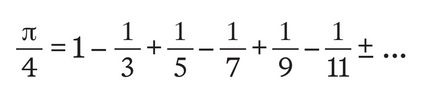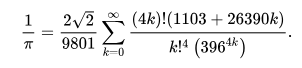The decimals of \(\pi\) go on forever, signalling the ratio of a circle’s round circumference to its straight diameter. The ratio is commonly written as \(\pi = 3.14159\ldots\), where the three dots symbolize “continuing without limit.” \(\pi\) is an irrational number, meaning it cannot be expressed as a fraction, and it is transcendental, meaning it is not algebraic—that is, it cannot be the solution of any non-zero polynomial equation with rational coefficients. Image by Gerd Altmann, of Pixabay.
By James Myers
Intuition is a uniquely human capacity that human-designed artificial intelligence has yet to demonstrate. Artificial intelligence is a remarkable product of the human mind and, with the help of technology, the mind’s capacity for logical intuition is leading to even more remarkable discoveries. Some of the most remarkable scientific advancements are rooted in, or depend on, the field of mathematics, where newly-uncovered connections are pointing the way to the hidden structures of the universe.
One significant demonstration of logical intuition was the discovery, in 2024, of a new formula for pi (represented by the Greek letter \(\pi\)).
Pi is the ratio of a circle’s circumference (which is round) to its diameter (which is straight). As many know, pi begins with the digits 3.14159… and goes on forever with decimals that have no repeating patterns in their digits. Pi is a crucially important value in mathematics, physics, and other sciences; for instance, Albert Einstein’s field equations, which underlie his famous discovery that E=mc², employ pi.
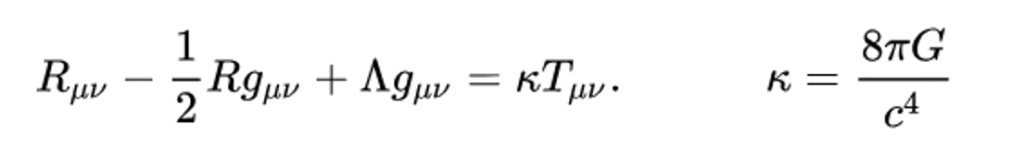
Underlying Einstein’s famous \(E = mc^2\) are his field equations, one of which is shown above. The equation uses the symbol \(K\). Einstein defined \(K\) as a fraction whose numerator consists of \(\pi\) multiplied by 8 and further multiplied by \(G\), the gravitational constant. The product of these three values is divided, in the denominator, by \(c\) (the speed of light) raised to the exponent 4, meaning that \(c\) multiplies by itself 4 times.
The new formula for \(\pi\) wasn’t discovered by mathematicians. Physicists Arnab Priya Saha and Aninda Sinha of the Indian Institute of Science discovered it while studying string theory, which posits that physical objects consist of tiny vibrating strings of energy rather than particles like electrons and protons which are the basis of the commonly held “standard model” of physics. Saha and Sinha, who weren’t practising mathematicians, used logical intuition to develop the mathematical formula that they published in May 2024 in the journal Physical Review Letters under the title Field Theory Expansions of String Theory Amplitudes.
The notation that Saha and Sinha used for their formula is mathematical, and notably uses the symbol λ (the Greek letter lambda, which has varying meanings in different physical applications) for a freely selectable parameter. No matter what value is given to λ, the formula always produces pi.
The new formula for \(\pi\) by Saha and Aninda Sinha begins with the number 4, which is added to an infinitely long sum (infinity is represented by the symbol \(\infty\)). The sum uses a variable labelled as \(n\), with values ranging from \(n = 1\) to \(n = \infty\). The infinite length of the sum is based on the fraction \(\frac{1}{n!}\) (meaning the number 1 divided by the factorial of \(n\)). The factorial \(n!\) means the multiplicative product of numbers from 1 to \(n\); for example, if \(n = 5\), then \(5! = 5 \times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120\).
The fraction is multiplied by two bracketed terms. The first term subtracts one fraction from another, and the second term uses a fraction from which \(n\) is subtracted. Note the positioning throughout the formula of the number 4 and its square root, which is 2.
Factorials have wide application—for example, in the mathematical constant \(e\), which is the infinite sum from \(n = 0\) to \(n = \infty\) of the same fraction \(\frac{1}{n!}\) that is used in the new formula for \(\pi\).
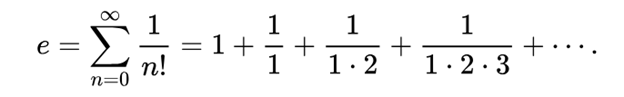
The mathematical constant \(e\) is the base of the natural logarithm. Like \(\pi\), \(e\) is irrational (meaning it can never be expressed as a complete fraction) and transcendental (meaning it can’t be expressed with algebra). In three-dimensional complex numbers, the Riemann Zeta function and the Gamma function—which frequently appear in physics—are analogues of \(e\).
The new formula for pi is a generalization of a 600-year-old discovery by Indian scholar Madhava, who lived from 1350-1425. If the value of λ in the new formula is set to infinity, the result is Madhava’s formula for pi:
The beauty of Madhava’s formula is the simplicity in its pattern of alternating negative and positive fractions, the denominators of which begin with the odd number 3 and thereafter increase by 2, which is an even number, in each successive step. The formula’s drawback is the large number of fractions required to produce a value that approaches pi; even after the alternating subtraction and addition of 100 fractions, the value is still not close. The more fractions there are, however, the closer the formula “approaches,” infinitely closely, the ratio pi.
(Note that a fraction can be expressed as a decimal, and decimals can be expressed as fractions. For example, the fraction \(\frac{1}{5} = 0.2\) and the decimals in \(\pi = 3.14159\ldots\) can be expressed as \(\frac{1}{10}\), \(\frac{4}{100}\), \(\frac{1}{1000}\), \(\frac{5}{10000}\), \(\frac{9}{100000}\), and so on.)

Archimedes’ method for estimating pi. Image: Wikimedia Commons.
An even more ancient intuition for the value of pi was famously that of Archimedes (ca. 287 BC to ca. 212 BC), who continuously circumscribed and inscribed polygons with circles. Being unable to square the circle, which was more recently proven impossible, with each successive step Archimedes increased the numbers of the polygon’s straight sides to fit more approximately within the roundness of the circle. The advantage of Archimedes’ method is that the area of the polygon can be measured exactly when the circle’s area can’t.
In Archimedes’ method, each time another straight edge is added to the others the difference in area between the polygon’s faces and the circumference of the circle reduces, and a more reasonable approximation of pi can be obtained.

Painting of the killing of Archimedes by a Roman soldier during Rome’s invasion of Syracuse. Some reports indicate that Archimedes was carrying mathematical instruments when he was slain for refusing the soldier’s orders. Painting, “The Death of Archimedes”, by Thomas Degeorge, 1815, on Wikipedia .
As mathematicians and others continue to gain more insights into the value of pi, it’s possible that some secrets of the universe might be unlocked.
The universe uses \(\pi\) in many of its physical functions. In fact, \(\pi\) appears in the mathematical expression for the universal Uncertainty Principle, first expressed by physicist Werner Heisenberg. The Uncertainty Principle says that the more we know of a particle’s position, the less we know of its momentum (which is the particle’s mass multiplied by the fraction \(\frac{\text{distance}}{\text{time}}\), as well as the direction in which the particle is moving). Conversely, the more we know of a particle’s momentum, the less we know of its position.
The Uncertainty Principle is a fundamental limit to human knowledge of physics. Mathematicians Earle Hesse Kennard and Hermann Weyl established the mathematical expression for the Uncertainty Principle using an inequality, rather than an equation, using \(\pi\) as follows:

The normal mathematical expression of the Uncertainty Principle has been expanded, above, to show the presence of pi, because \(\hbar = \frac{h}{2\pi}\), and to illustrate that 2=(1+1). In the mathematical inequality, the symbol σ represents the standard deviation from the mean, x represents spatial and temporal position expressible by 4=(1+1)(1+1) points, p represents physical momentum, and h represents the Planck constant. The Planck constant is the minimum measurable unit of the physical universe. The inequality of the product of the standard deviations of spatial/temporal position and momentum, shown on the left-hand side, to the Planck constant in the fraction shown on the right-hand side, establishes a topology for uncertainty.
The human intuitive skill owes much to the brain’s superior ability for pattern recognition, and mathematics is full of patterns.
At its most fundamental level, the process of living requires knowledge of numbers, and children’s first tools for counting numbers are often their fingers. We learn to count the hours in a day, the minutes in an hour, the seconds in the minutes, and the order in which everything happens in those intervals. We measure changes in numbers, like the value of a currency or the rapid increase in the cost of food and housing, because changes like those directly influence our daily living.
Since mathematical intuitions are based on patterns in numbers, which are fundamental to living, the intuitions are even accessible to people who are not trained mathematicians.
A famous example of incredible mathematical intuition from someone who wasn’t formally trained in mathematics is Srinivasa Ramanujan. Little more than 100 years ago, Ramanujan developed theorems and formulas that physicists are now using to study the mechanics of black holes.
Ramanujan was born in India to a mother who kept house and sang at a local temple and a father who worked as a clerk in a sari shop. With no mathematical background or formal training, Ramanujan was brought to Cambridge University to study with the great mathematician G.H. Hardy. In his notes, Hardy wrote that Ramanujan had produced groundbreaking new theorems, including some that “defeated me completely; I had never seen anything in the least like them before.”
One of the dozens of innovative formulas for pi discovered by Ramanujan was:
What’s the brain’s secret for logical intuition?
Intuition may be a consequence of the way the brain can store massive amounts of information. Neuroscientist Daniel Bor has written that when our brains convert sensory and other data into a pattern or rule, “near-magical results ensue. We no longer need to remember a mountain of data; we need to only recall one simple law.”
Efficiency is a crucial feat for the brain, which comprises less than 2% of the body’s mass but uses up to 25% of its energy, and it’s a feat that makes the human mind incredibly versatile and creative.
One 2014 study published in Frontiers in Neuroscience, entitled Superior pattern processing is the essence of the evolved human brain, notes that “Language is the quintessential example of the evolved SPP [superior pattern processing] capabilities of the human brain as it involves (once learned) the instantaneous conversion of sounds to visual symbols, and vice-versa.”
The human brain, depicted from below. Image by Dr. Johannes Sobotta, Atlas and Text-book of Human Anatomy, Volume III Vascular System, Lymphatic system, Nervous system and Sense Organs, on Wikipedia.
The outer layer of the brain, called the neocortex, is thought to be responsible for the brain’s pattern recognition superpower.
The neocortex is an incredibly dense layer that accounts for 80% of the brain’s weight, with neurons interconnecting through a vast number of folds. Emotional responses, which strengthen particular memories, can reinforce pattern recognition. (For more on the role of emotions, see our feature Essential for Human Memory, Emotional Processing is a Weakness of Artificial Neural Networks. We Look at the Reasons Why).
The molecular and cellular mechanisms that provide the human brain with superior pattern recognition are not fully understood, but logical intuitions like those of physicists Saha and Sinha in developing a new formula for pi help to illustrate Daniel Bor’s statement about the efficient power of the human brain. We develop general formulas that replace mountains of data with the same information but in a very compact form.
The brain packs tremendous power with little mass in a very compact space. Each of the 85 billion neurons in the human brain connects to an average of 7,000 other neurons, for a total of about 600 trillion connections with exponential potential in our heads—which is far greater than the number of circuits imaginable for any computer or AI application or LLM.
Why is mathematical logic a particular object for intuition, even for those like Srinivasa Ramanujan who did not receive rigorous mathematical training before devising the most incredible formulas? Perhaps it is because patterns are in numbers everywhere around us, and even in our ideas.
As G.H. Hardy wrote in his essay A Mathematician’s Apology, “A mathematician, like a painter or a poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas. A painter makes patterns with shapes and colours, a poet with words.” Comparing mathematical output to poetry and paintings, Hardy wrote that, “A mathematician, on the other hand, has no material to work with but ideas, and so his patterns are likely to last longer, since ideas wear less with time than words.”
Who knows who will come up with the next ideas that unlock some of the biggest mysteries about how the universe operates?
What we do know, however, is that computer algorithms don’t come up with ideas, because algorithms do as they are programmed by humans to do and anything that doesn’t follow a program can’t be called an algorithm. Ideas are human innovations, and products of human intuition for patterns. If a circle is the most fundamental of patterns, then more insights into the ratio of round to straight, which we call pi, could well produce ideas that reveal wonders far greater than any algorithm.