
Illustration by Gerd Altmann, Pixabay.
By James Myers
Beginning and end are opposite limits that confront us in two ways practically every moment of our lives. But what if there really is no particular beginning or true end to anything?

Dr. Julian Barbour, photographed in 2008 by Boris Barbour, Wikipedia.
Physicist Julian Barbour proposes a radical redefinition of time that could have profound consequences for our understanding of quantum mechanics and computing.
Our five senses tell us that physical things are limited by a beginning and end in space, and that events have beginnings and ends in time. But if the universe itself has no limits to space or time, according to Barbour that means time is not an inherent feature of reality. What we think of as time, he says, is actually our experience of the increasing complexity of a boundless universe.
Barbour’s insights were built on the work of Nobel Prize laureate Paul Dirac (1902-1984), who advanced the ideas that events exist in absolute simultaneity and that symmetry in four dimensions of space and time is not fundamental to the universe. As Barbour stated in a podcast interview, “If Dirac thinks there is a notion of absolute simultaneity, then what is time? And I’m still thinking about it now.”
Measuring changes arising from events, including quantum interactions, occurs over time.
So, what is time, and where should measurements of quantum events begin and end?
In the perspective of absolute simultaneity of events, nature doesn’t operate “from past to future,” and we can’t accurately pinpoint the cause and effect of anything—that is, if we want to trace an event or a physical thing to its very beginning. Universal time doesn’t consist of “was” and “will be;” instead, time simply and simultaneously “is.”
Absolute simultaneity would also mean that instead of the single arrow of time that we experience, where according to the second law of thermodynamics physical objects begin in a state of order and end in maximum disorder, there could actually be two “arrows” of time. With their opposite limits, both arrows would weave increasing complexity into a universe full of probabilities in its quantum interactions.
Knowing the universal limits of most things wouldn’t make a difference to the way we experience our daily lives; for example, our workdays would still have two limits, beginning at 9 am and ending at 5 pm. But pinpointing cause and effect in tiny quantum interactions is crucial to maintaining stable quantum computing circuitry and overcoming the problem of decoherence that has posed the biggest challenge in the quest to develop a fully functional quantum computer.

Physicist and priest Georges Lemaitre proposed that the universe was formed from a “primeval atom,” and together with astronomer Edwin Hubble observed that in our expanding universe, galaxies recede from the observer with a velocity proportional to their distance. Image: Wikipedia
Is it time to revisit the Big Bang?
The idea that there could be two arrows of time is gaining traction. As we reported last month in Does Time Flow in Two Directions? Science Explores the Possibility—and its Stunning Implications, a recent mathematical analysis has established that the laws of physics could work just as well in reverse as they do in the one direction of our physical experience. The mathematics don’t mean that we could physically experience something as unbelievable as a shattered glass reassembling itself. However, they imply that at the most fundamental level of the quantum, the laws of physics would operate like a pendulum, oscillating equally in two directions from a fixed point.
In other words, while our experience in four dimensions of space and time is asymmetric, because physical events aren’t reversible, symmetry and reversibility are at the very foundation of time itself apart from the dimensions of space.
What does this say about the Big Bang, as the most asymmetric of event of all time?
We continue to experience the Big Bang’s effects, but we can’t discern a corresponding, symmetric cause. The problem in this is that symmetry of cause and effect is a key principle of Newton’s third law of motion, which says that for every action there’s an equal and opposite reaction.
Since it was first proposed nearly a century ago, the Big Bang theory has become a widely accepted explanation for the beginning of space and time in the universe. The theory holds that the universe, now thought to consist of a trillion or more galaxies, exploded from a single point 13.8 billion years ago. The cause of the explosion is unknown.
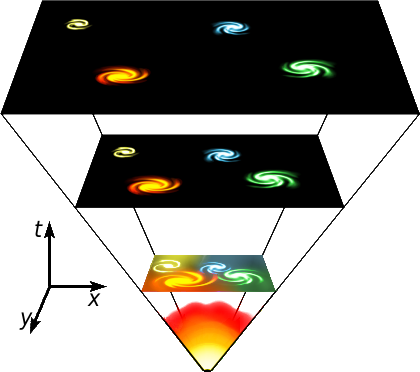
The emergence of a “flat” universe from a fiery Big Bang that continues to propel galaxies in space and time. Illustration by Gnixon, on Wikipedia.
Questions about the Big Bang linger. If the concept of “universe” describes all that ever was, is, or will be, how could it have been derived from anything else? And why is the density of plasma in the cosmic microwave background, which is the shroud that blocks our telescopes from measuring space and time during the first 370,000 years of the universe, uneven—when the second law of thermodynamics says that all physical things begin in a state of maximum order and end in disorder?
In the recent mathematical analysis establishing the potential for two arrows of time, the study’s co-authors observed that we would live on one of the two arrows that’s asymmetric and where energy dissipates with entropy from “time zero” of the Big Bang. They state that the Big Bang also gave birth to another arrow of time, one that we can’t perceive because of its symmetry that provides no differences for perception to register.

Image of the cosmic microwave background of radiation assembled in 2012 using 9 years of data from the WMAP probe. The different colours denote areas of varying densities. WMAP also observed that 95% of the early universe is composed of dark matter and dark energy, and the universe is within 0.4% of being “flat” with no overall curvature. Image by NASA on Wikipedia.
With events occurring in absolute simultaneity, how can we measure the order of cause and effect in quantum interactions?
If there are no universal boundaries and therefore no beginning or end for space and time, it could radically change our understanding of the thermodynamic processes of particles at the quantum level. The existence of two arrows of time would require a reformulation of the second law of thermodynamics, long held as a bedrock principle about the order of cause and effect in time.

Rudolf Clausius, who coined “entropy.” Photograph by Theo Schafgans (1859-1907), in Wikipedia.
The state of disorder that marks the end limit of all physical things under the second law of thermodynamics is called maximum entropy. Entropy is the term coined by physicist and mathematician Rudolf Clausius in 1865, intended to mean “the transformation of energy.” Barbour expands on the concept of entropy, which he says would apply to a bounded universe, with what he calls “entaxy.” Whereas the disorder of entropy is thought to increase over time, in Barbour’s concept of entaxy it is complexity, rather than disorder, that increases from moment to moment in an unbounded universe that is itself without limits of beginning and end.
If we imagine complexity like a tree with branches that continuously sprout new shoots, time in this sense would be our journey through the ever-increasing knots of branches and offshoots.
The concept of entropy assumes an ability to measure the point of equilibrium between things like pressure, temperature, and volume that drive transformations of energy. Clausius conceived of entropy using an analogy of actions of particles within a container, like a box, where over time the forces driving change will even out in equilibrium, when there would be no further change. What if the universe isn’t like a box, Barbour asks, and unlike a box has no defined limits?
Barbour suggests that we could imagine the second law of thermodynamics not as entropy within a box but the continual spreading, or diffusion, of energy with increasing complexity in a universe that has no inherent limits.
Redefining quantum measurement with Barbour’s “Janus-point systems”
Barbour’s latest book, The Janus Point: A New Theory of Time, sets out his ideas that time does not flow with a single past or future direction, and that the universe is not expanding but instead changing shape as increasingly complex structures form. The theorized Janus point is like a hinge, on either side of which change occurs asymmetrically with time. The opposite sides of the Janus point each provide a solution that has a single past and two futures.
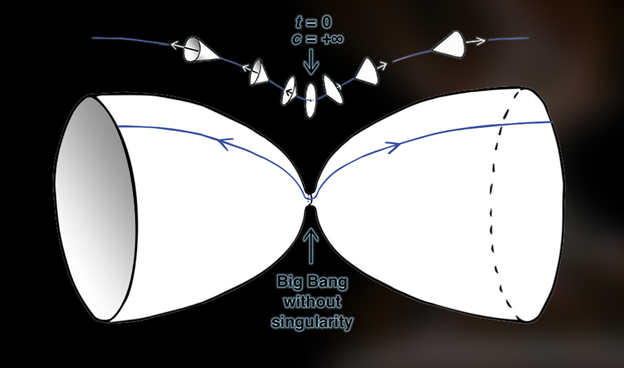
Illustration of the Big Bang as a Janus point. Unlike conventional concepts of the Big Bang, time does not go to zero in the Janus point theory, but is squeezed down to a narrow ‘neck’ which is the point from which opposite arrows of time emerge. Image: Dr. Jean-Pierre Petit.
“Observers in either half [of the Janus point] must find an arrow of time,” Barbour wrote in a 2015 presentation (see pdf).
Whereas the traditional concept of entropy has energy moving from order to disorder, Janus-point systems are centered on a point of disorder from which the branches of complexity emerge with a specific ordering in opposite directions. Entaxy, Barbour’s analogue for entropy, decreases as distance in both directions from the Janus point increases. The decrease in entaxy is a measure of the system’s increasing complexity and variety.
The key to quantum measurement, in this context, would be the location of the Janus point and the ratios that emerge in opposite directions.
In an interview on the Closer To Truth channel (see YouTube link above), Barbour used the analogy of real numbers, which are infinitely dense, to explain the Janus point: “Just think about ordinary real numbers with their decimal expansion. The decimal expansion can go on forever, so there’s always going to be a difference between one decimal place and the next one. You could imagine two real numbers looking at their decimal expansion: there’s always a difference between them.” (Note that “decimal” is another way of saying ratio, or fraction).
The measurement problem arises from thinking of the universe as a closed box, Barbour says, and even our measurement of the universal minimum Planck length depends on reference to the wavelength of energy in caesium atoms, which are the basis of atomic clocks. (For more on caesium atoms and atomic clocks, see our article New Ways of Measuring Time Increase Precision and Technological Potential).
Barbour states, “All around us we see measuring rods and clocks, and we think they’re absolute, but there can’t be a measuring rod outside the universe. We have to look for measuring rods within the universe, and if the things that we take to be measuring rods—there are some that are ‘so’ long and others that are ‘that’ long—there will be a difference between them, even if you might imagine that they’re all getting smaller, but that difference remains. It’s that ratio that is always the one that counts: 2 is always less than 3.”
“There is always meaning in ratios.” —Julian Barbour
Overcoming the problem of quantum measurement: will two arrows of time from a single Janus point provide a key?
Measurement of cause and effect in quantum systems and their circuits is notoriously difficult for several reasons, prime among which is the observer effect (see The Observer Effect: Why Do Our Measurements Change Quantum Outcomes?). The observer effect is the unexplained phenomenon in which the outcome of an observed quantum interaction differs from the outcome of the same interaction that has not been observed. Why does observation, which involves no physical force, affect a physical outcome?
Another measurement problem in quantum interactions arises from superposition and entanglement.
These phenomena, which don’t apply in the physical world that we can see, arise from the fact that a quantum exists in two states simultaneously (unlike a computer bit that can exist in only one of an “on” or “off” state at a single time), and two quanta connect (“entangle”) such that the pair share the same state without the passage of time (unlike the time required to switch states between computer bits). How can cause and effect among two things, each in two states and with no time difference separating them, be measured?
Bell’s theorem currently provides a key basis for measuring quantum entanglement.
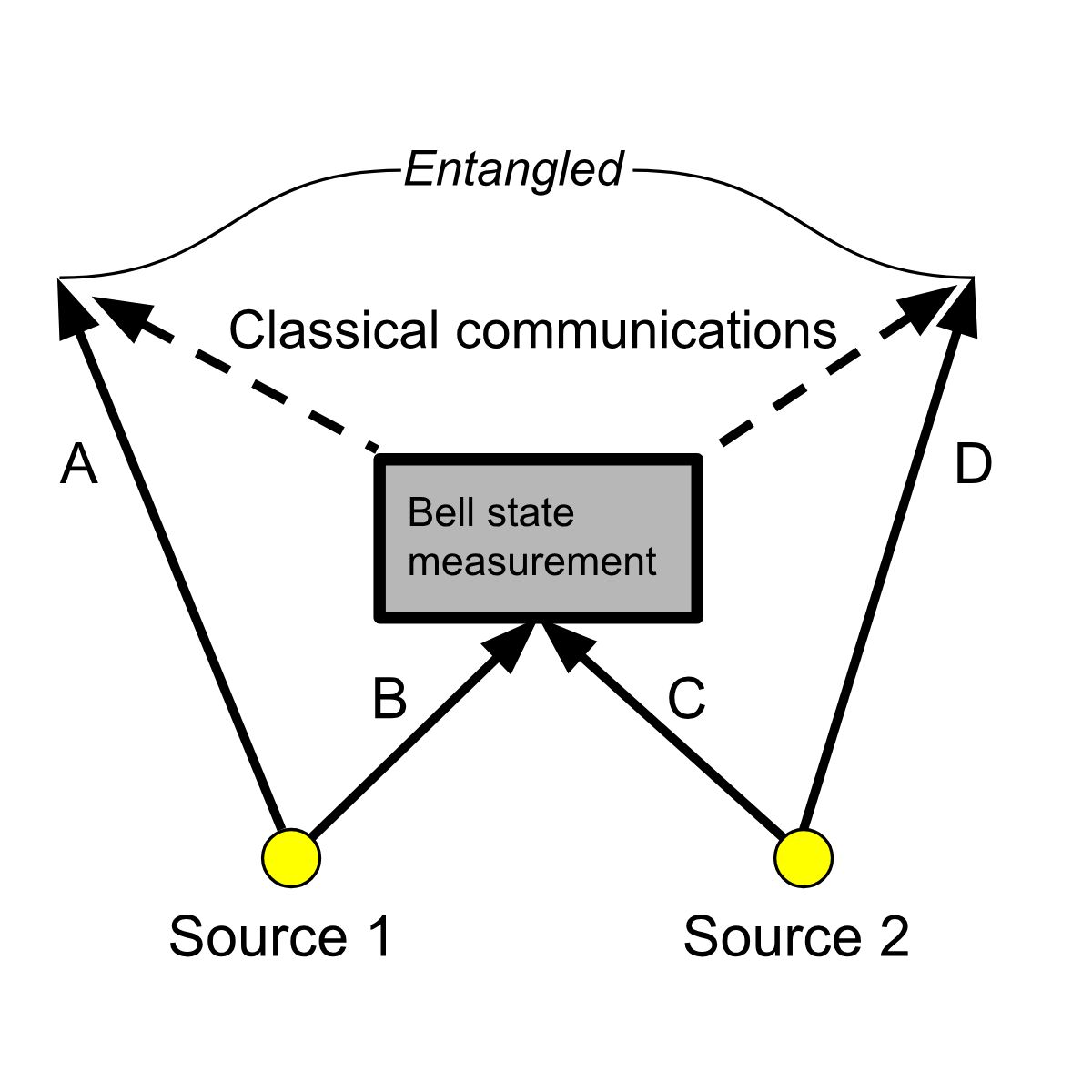
Illustration of quantum entanglement and Bell’s inequality measurement by johnjbarton, on Wikipedia.
First introduced by physicist John Stewart Bell in 1964, the theory establishes mathematical limits for correlated probabilities measured between separate particles, on the assumption that the particles are influenced by unknown variables only in their local environment and not more globally.
Measuring particles far enough apart, so that no signal at the speed of light could communicate between them, Bell’s theorem fixes a point of inequality. The inequality point is the threshold, or constraint, beyond which local variables could not influence the behaviour of a particle. Crossing the threshold is evidence of quantum entanglement, indicating the non-locality of cause and effect that does not depend on the speed of light and passage of time required for observable physical changes.
Bell’s inequality has undergone numerous experimental tests and refinements, consistently demonstrating its effectiveness in gauging quantum entanglement. What it can’t fully account for, however, is the order of cause and effect among two entangled quantum particles. That’s because they are both in a state of superposition, which encompasses all possibilities, and their history of entanglements and decouplings is impossible to trace when every quantum is like every other quantum.
Could tracing the ratios among groups and sets of quanta (the plural of quantum) lead to the Janus point, where the quantum arrows of time are exactly opposite? Would this provide a means for maintaining stable quantum circuits, reducing or eliminating the problem of decoherence? Could it be a point of reference to determining cause and effect in quantum interactions, on the basis of ratios between two arrows time—once an arrow of time is determined by an observer with knowledge of which side of the Janus point the arrow is measured?
The possibilities for Julian Barbour’s unconventional theory are intriguing. Now that a mathematical basis for two arrows of time has been established, perhaps a deeper investigation into the point at which the arrows separate as opposites will yield crucial information about cause and effect among entangled quanta in superposition.
Craving more information? Check out these recommended TQR articles:
- Digital Sovereignty: Cutting Dependence on Dominant Tech Companies
- Does Time Flow in Two Directions? Science Explores the Possibility—and its Stunning Implications
- Do We Live Inside a Black Hole? New Evidence Could Redefine Distance and Time
- What’s Slowing the Expansion of the Universe? New Technologies Probing Dark Energy May Hold the Answer
- The Corruption of Four-Dimensional Humanity with Two-Dimensional Technology




