
Snowflake with perfect symmetry.
Every snowflake that has ever formed in nature is unique.
Although scientists may artificially create very similar patterns, even the most controlled conditions in a laboratory will hardly make two perfectly identical snowflakes. These water crystals can spontaneously take many forms, like simple stars, prisms, columns, and cups. But why are they all different from each other, apart from their shared intricate nature and six-fold symmetry? Surprisingly, the answer has less to do with randomness and more to do with the processes of physics.

Needle Snowflakes
The different patterns in snowflakes occur due to changes in growth conditions.
Snowflakes form when water vapor rises in the atmosphere, cools down and forms tiny droplets around dust particles. When the temperature is sufficiently low and one droplet freezes, its water molecules arrange themselves to form a hexagonal crystal. The hexagonal pattern derives from the peculiarity of the structure of the water molecule, the hydrogen bond – since water consists of two hydrogen atoms and one oxygen. The crystal grows as new droplets are incorporated, taking approximately 30 to 45 minutes and a hundred thousand droplets to make a single snowflake. Importantly, its format will depend on what growth conditions are present in the precise moments of freezing. Changes in atmospheric conditions such as temperature and water saturation may profoundly affect the snowflake format.
The hydrogen bond “Interactions that form between a hydrogen with a partial positive charge and a more electronegative atom, such as oxygen. (…) Polar molecules, such as water molecules, have a weak, partial negative charge at one region of the molecule (the oxygen atom in water) and a partial positive charge elsewhere (the hydrogen atoms in water). Thus, when water molecules are close together, their positive and negative regions are attracted to the oppositely-charged regions of nearby molecules, which makes it bond. (…) Water owes (its) unique properties to the polarity of its molecules and, specifically, to their ability to form hydrogen bonds with each other and with other molecules”. Khan Academy.
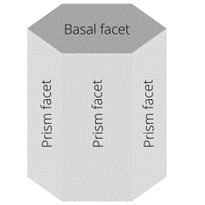
The hexagonal prism of ice has two basal facets and six prism facets.
A facet is a face of the crystal, a flat surface of the snowflake.
The hexagonal prism of ice has two basal facets and six prism facets. If the basal facets grow faster than the prism facets, the ice crystal will take the form of a column. If, on the other hand, the prism facets grow faster, then we get a flat (or plate-like) snowflake. “Once there is a seed crystal, nearby water droplets evaporate and deposit water molecules onto the growing snowflake. Since the corners of the hexagonal prism stick out farther into the humid air, they grow faster, [which makes them] extend even farther, so they grow even faster, in a positive feedback loop. This gives rise to six radial branches. At the corners of these branches, additional branches can form for the same reason”, explains Dr. Derek Muller.
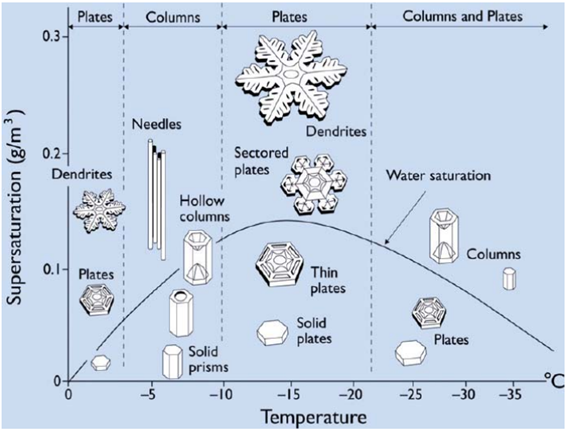
The Nakaya Diagram.
The Nakaya Diagram allows us to understand roughly how each snowflake has formed.
The diagram was named after Ukichiro Nakaya, who in the 1930s discovered that the different types of snowflakes do not all occur under the same conditions, but are, instead, determined by temperature and moisture level. But it is not a simple pattern. Rather, as the temperature lowers, from, say, -2º Celsius, to -20º Celsius, plates (i.e. flat snowflakes) can give space to columns and needles, and then plates again, and then plates and columns. The reason for these changes, nevertheless, remained a mystery… until recently.
Dr. Kenneth Libbrecht, a physics professor at Caltech long dedicated to the subject, has built his version of the chart. He believes he now has an answer, and it lies with the so-called nucleation barriers. “Anytime you have a crystal, the reason why you get these smooth flat facets is because it’s not easy to grow more crystal on top. There are so-called nucleation barriers. What you need is a critical density of additional molecules of the substance before they can come together to form a little island that is stable enough to grow and add another layer onto the crystal”, explains Dr. Muller. The catch revealed by Dr. Libbrecht is that the nucleation barrier for the basal facets is different than that of the prism facets: “If the nucleation barrier is lower for the prism facets, then they grow faster, and you get plate-like structures. If the nucleation barrier is lower for the basal facets, then they grow faster and you end up with column-like structures”, he explains. Since the nucleation barriers of ice are a function of temperature, this explains why at different temperatures we see different shapes.
“Nucleation is the process where droplets of liquid can condense from a vapor, or bubbles of gas can form in a boiling liquid. Nucleation can also occur in crystal solution to grow new crystals. It is seen in gases when tiny bubbles coalesce into larger ones. In general, nucleation is a self-organizing process that leads to a new thermodynamic phase or a self-assembled structure. [For instance,] dust and pollutants provide nucleation sites for water vapor in the atmosphere to form clouds, [and] seed crystals provide nucleation sites for crystal growing”. [Thought Co.]
Dr. Libbrecht hypothesized that these nucleation barriers are valid only for large facets, while for narrow facets the nucleation barriers would be different. Put simply, the narrow edge provides a lower nucleation barrier than a large facet, and the barrier of narrow edges differs according to type: for narrow basal facets, it occurs at around -4º Celsius, while for narrow prism facets it’s around -15º Celsius. This explains why snowflakes take the form of plates at -2º C, then columns at around -5º C, and then plates again at -15º C. Dr. Libbrecht’s experiments have provided robust support for his hypothesis.
This explains why snowflakes are so intricate. “The temperature and humidity at each moment of growth determine the structures formed at that moment. The symmetry you see is not because one side somehow knows what the other side is doing, but because both sides of a single snowflake grow in the exact same conditions”, explains Dr. Muller.

Examples of different shapes of snowflakes.
On the other hand, each snowflake takes a unique path and experiences a unique set of conditions, which explains why no two snowflakes are alike.
In the lab, Dr. Libbrecht has managed to create what he calls identical twin snowflakes, which are very similar but never completely equal snowflakes. As he points out, can really anything complex in nature be completely the same? “No two trees are alike, no two grains of sand are alike, no two anything are alike. Anything that has any complexity is different from everything else, because once you introduce complexity, then there’s just an uncountable number of ways to make it”, observes Dr. Libbrecht. For instance, growing two snowflakes close together in the lab may make them look alike since they’ll share the same conditions. But their proximity might also mean that they’ll end up competing for moisture, stunting their growths.
Now, for the first time, scientists are using deep learning to predict something so complex that is how ice crystals form in the atmosphere – the first steps in the formation of clouds and rain. In a paper published in August 2022, Dr. Pablo Piaggi and co-authors explain that “Until recently, simulating ice nucleation with quantum accuracy was deemed impossible due to the prohibitive computational cost of quantum-mechanical calculations. Recent progress enabled by machine learning has made these calculations tractable and thus greatly extended the field”. In time, they hope to increase the accuracy of weather and climate forecasting, by modeling nucleation processes in more realistic environments.
“Deep learning is a subset of machine learning, which is essentially a neural network with three or more layers. These neural networks attempt to simulate the behavior of the human brain—albeit far from matching its ability—allowing it to “learn” from large amounts of data. (…) Deep learning drives many artificial intelligence (AI) applications and services that improve automation, performing analytical and physical tasks without human intervention. Deep learning technology lies behind everyday products and services (such as digital assistants, voice-enabled TV remotes, and credit card fraud detection) as well as emerging technologies (such as self-driving cars)” IBM.

Koch Snowflake.
One interesting fact about snowflakes is that they do not follow a fractal geometry pattern, although it might seem they do because of their intricateness and the fame of the Koch Snowflake – which is not a real snowflake. Fractals are geometric shapes that are self-similar, meaning that, as you zoom in to any part of the pattern, you will tend to see a “smaller” copy of the entire shape. Benoît Mandelbrot, who first coined the term in 1975, was the first to create fractals using computers. Among other definitions, he stated that a “fractal is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole”.
“The Koch snowflake is a fractal curve, also known as the Koch island, which was first described by Helge von Koch in 1904. It is built by starting with an equilateral triangle, removing the inner third of each side, building another equilateral triangle at the location where the side was removed, and then repeating the process indefinitely”. Math World.
Fractal patterns can have different degrees of self-similarity, and not being limited to geometric patterns they can even describe processes in time. Examples of fractal-based systems are abundant in nature. For instance, fractals allow plants to maximize their exposure to sunlight, and the human cardiovascular system to efficiently oxygenate the entire body. As Mandelbrot famously wrote in 1982: “Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line”.

The Romanesco Cauliflower.
In spite of the infinitely differing shapes we find in snowflakes, as well as in the fractal patterns that appear elsewhere in nature, they share one important trait: they remind us of how complex the natural world really is.



