Newton’s Cradle, named after Isaac Newton, demonstrates universal laws of conservation of energy and momentum with classical mechanics. Image by Jonathan Thorne
Our understanding of an object’s behavior and interactions depends on the scale and attributes that we observe. Characteristics observed at a larger scale differ significantly from those detected at the smallest possible level of detail.
While classical physics is best suited to describe the behavior of everyday objects like a basketball bouncing on the floor, general relativity is better at interpreting the physics of massive objects like the collision of two stars, and quantum physics is required to comprehend the behavior of the tiniest subatomic particles. This disparity arises because different rules appear to predominate in different physical scales. As a result, new properties of physics emerge from the discovery of systems that existing knowledge cannot adequately explain.
When Dr. Ryo Hanai and Dr. Peter Littlewood, researchers at the University of Chicago, studied quasiparticles a few years ago, they encountered an unexpected finding. They identified an unexplored knowledge gap of phase transitions in a particular type of quantum system.
A phase transition is a change in the physical state of a substance, for example as it moves between gas, liquid, solid, or plasma states. Using mathematical concepts and the help of collaborators to analyze the data, they explored the rules behind the behavior of systems that are not in equilibrium. In the process, they also tackled questions regarding states of matter and even physical symmetries, opening up new avenues and possibilities for research in mathematics and physics.
“A quasiparticle is a collection of quantum characteristics among particles operating in their own, particle-like way. Unlike fundamental bits of matter like electrons and quarks, quasiparticles aren’t members of the standard model. And unlike neutrons, protons, or even atoms and molecules, they aren’t independent structures floating about on their own in free space. Similar to fundamental particles, though, quasiparticles have fundamental properties like charge and spin.” ScienceAlert.
Newton’s three laws of motion are the foundation of classical mechanics.
They describe how an object moves, what forces act on it, and how energy changes.
The first law states that if no forces are acting on the object or all existing forces are balanced (i.e., in equilibrium with zero net force), the object is either at rest or its existing motion remains unchanged. Conversely, the second law states that if a net force acts on an object, it will accelerate. Finally, the third law states that when two bodies exert forces on each other, the forces between them are equal in magnitude and opposite in direction.
This third law is known as the law of action and reaction. It establishes, for example, that the force that a table exerts on the ground by its weight is reciprocated by the ground with an equal and opposite force on the feet of the table. In other words, this law establishes the reciprocity of systems in equilibrium where there is neither inflow nor outflow of energy. Mathematically, this allows researchers to model the conditions that favor phase transitions of matter, such as water freezing.

Sir Isaac Newton (1642-1727) is one of the greatest mathematicians and physicists and one of the most influential scientists of all time.
Newtonian systems, however, are only a limited subset of systems, and classical mechanics is far from a complete guide to understanding the multitude of systems that exist.
Systems that are not in equilibrium often defy Newton’s laws of motion. Examples of such systems include lasers, cars, and even living organisms. In order to maintain their stability while not in equilibrium, these systems rely on a continuous supply of energy, whether through the addition of photons, the burning of fuel, or the metabolism of organic matter.
When out of equilibrium, this Newtonian reciprocity between the components of the system often breaks down.
Non-reciprocity in a system exists when its parts interact with each other in different ways, depending on the order of action – for example when the way component A acts on component B differs from how B acts on A. Flocks of birds are a good example of this. During flight, each bird reacts only to the movement of the birds in front of it, so the way two birds interact is non-reciprocal. This kind of non-reciprocity is often found in the brain’s neuron networks, particles in fluids, and even social groups.
Structurally, these non-reciprocal relationships have enormous implications for phase transitions, as they affect the resulting collective behavior of the system. Moreover, in systems that are out of equilibrium, components often have their own energy source. These complex dynamical systems are beyond the reach of statistical mechanics and pose a challenge to our current understanding of the phases of matter.
While conducting experiments with polaritons, a quasiparticle that can form the Bose-Einstein condensate (BEC), Dr. Hanai and Dr. Littlewood observed that the system used to create the BEC requires a constant supply of light as photons continuously escape it. Since this system requires a continuous supply of energy to maintain its stability, we can say that it is out of equilibrium. They became intrigued by how being out of equilibrium affects the phase transitions and how the transitions could affect the symmetry of such systems.
Working with Dr. Vincenzo Vitelli, a professor at the same University, the team realized that phase transitions in out of equilibrium quantum systems represent singularities known as exceptional points. Such points occur when two or more properties in a system collapse into one and become indistinguishable. The system’s behavior at those points differs significantly from nearby points. Exceptional points often describe strange phenomena in systems, and the team has discovered that they control phase transitions in non-reciprocal systems.
Another critical aspect of phase transitions relates to the symmetries of the system.
Conformal invariance is the name given to a set of three symmetries thought to be a universal feature of phase transitions in physical systems. The symmetries are: Translational symmetry, meaning the object stays the same when shifted; Rotational symmetry, meaning the object stays the same when rotated; and Scale symmetry, meaning the angles of the object stay the same when its size changes.
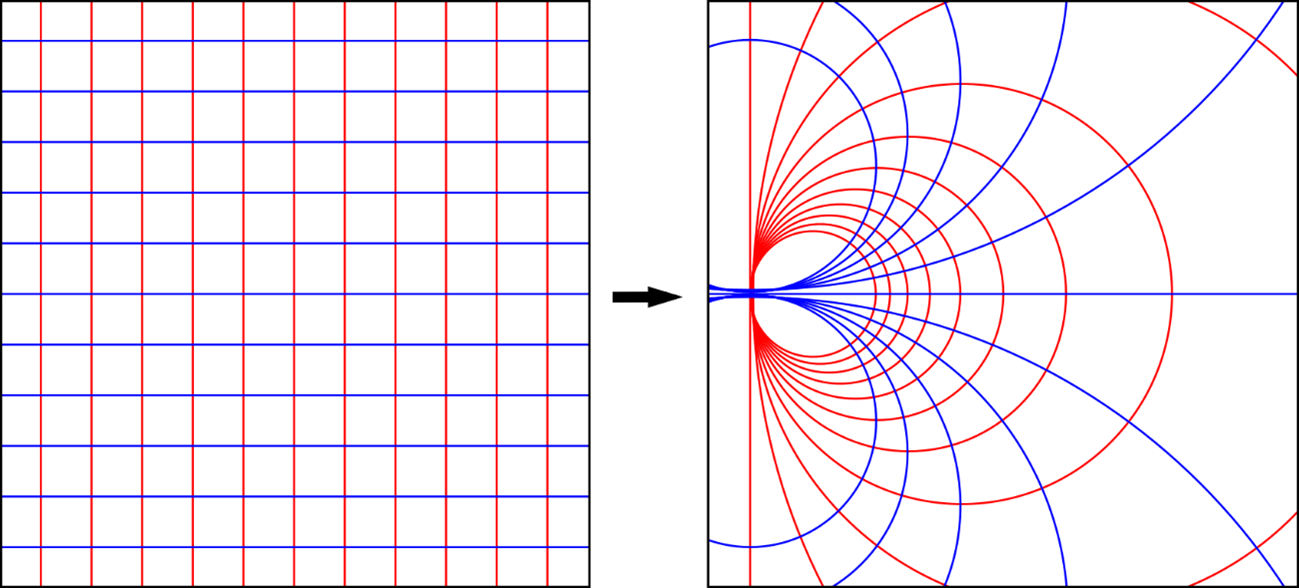
Example of a coordinate grid subjected to a special conformal transformation, which preserves angles by mapping straight lines to lines or circles. Adapted from Lokal_Profil1,2.
Magnetic materials provide a great demonstration of the symmetries that arise from the individual behaviors of the components of a system.
Each atom in a magnetic material has its own strength and orientation – its magnetic moment. The atoms collectively generate the system’s magnetic field by pointing in the same direction, which means that the system has no symmetry. However, when the system is heated, the magnetic moments of the atoms are thrown into confusion, restoring the symmetry of the system and canceling its magnetic field.
Similarly, we can describe a flock of birds or a school of fish as asymmetric because of the alignment of the individuals in these systems. But unlike magnetic materials, these systems are not in equilibrium and cannot be fully explained by statistical mechanics. Each individual adds energy to the system (by eating), which leads to changes in the system’s behavior.
In 2019, Dr. Hanai’s team proposed a new universal mechanism for how exceptional points generate phase transitions in quantum dynamical systems. At the transition point, different phases are often mathematically indistinguishable. For systems in equilibrium, this is defined as a critical point. The same phenomenon occurs at exceptional points for systems out of equilibrium, implying common properties between the two concepts.
The researchers realized that although they were studying a quantum state of matter, their equations did not depend on quantum mechanics. They could also potentially apply the connections between phase transitions and exceptional points to classical systems. Working with Dr. Vitelli and Dr. Michel Fruchart, a researcher in Vitelli’s lab, they began to investigate whether they had encountered a universal principle or law underlying systems that defy the law of conservation of energy.
To investigate the principles that link phase transitions to non-reciprocal interactions, the team created a system with robots programmed to interact non-reciprocally.
The system consisted of two types of robots: blue and red robots. The researchers programmed them to interact based on their colors: blue robots would align with blue robots, but not with red robots; conversely, red robots would align with both red and blue robots. The non-reciprocity between blue and red robots guaranteed that neither individual would ever reach its ideal state.

The robots used in the experiment to observe phase transitions. Adapted from Fruchart et al. (2021).
When the robots were scattered on the floor and turned on, their collective behavior formed a defined pattern almost immediately.
The interactions between the robots caused them to begin turning in the same direction on basically the same spot. This spontaneously coordinated collective behavior of the robots illustrates a phase transition for an out-of-equilibrium system, breaking the symmetry of the system just like the exotic quantum condensates that Dr. Hanai studied using polaritons.
The team is gradually building on its newly acquired knowledge, making connections between different fields to study the behavior of out-of-equilibrium systems. Dr. Vitelli emphasizes that this new work highlights the limitations of the current language of physics and mathematics for describing these dynamical systems. These limitations require a new framework to describe these systems in the language of dynamics rather than through analysis based on energy, given that the flow of energy in these systems makes the latter significantly more complex. For that, we may need new mathematics.
Researchers are still in the early stages of this new path, and so far, it appears that what they have found may be just the tip of the iceberg. They suggest that, beyond reciprocity, there are several phenomena in dynamical systems that could be described using the new framework. Research on the scope of this framework is already underway to develop a general theory of collective phenomena in those systems.
This new framework could help us better understand the behavior of complex dynamical systems ranging from exotic quantum states of condensed matter to the human brain.
The possibilities are vast. As researchers explore these new areas of knowledge without knowing how far they will go, the excitement can be expressed in the words of the mathematician Dr. Robert Kohn of the Courant Institute of Mathematical Sciences at New York University: “Here’s a sandbox that we haven’t noticed so far, and here’s a list of things we might do.”