Artistic rendering of uncertain interactions among wave functions in differing positions and velocities. Image Gerd Altmann, Pixabay.
By James Myers
Although an exact definition of time remains elusive, our perception of time consists of events, and events are combinations of cause and effect. Improving our understanding of the order of cause and effect in the microscopic realm of the quantum, which operates with probabilities, could provide new methods to control circuits in quantum computers.
In a recent breakthrough, researchers have succeeded in leveraging tensor networks, which are used by quantum scientists in assessing multiple quantum connections, to calculate the distribution and density of probabilities in turbulent fluids. Their methods, which we discuss below, could open new avenues for achieving stable quantum circuits.
Circuit control is a crucial step in unleashing the potential power of a fully-functioning quantum computer. Quantum circuits are delicate and prone to disconnection, a problem that scientists are seeking to resolve with much recent progress (see, for example, our February article, Breakthroughs in Teleportation and Topological Qubits Bring Quantum Computing Closer to Reality).
The quest to understand quantum cause and effect relationships for stabilizing quantum computing circuitry is not new. As Jean-Philippe W. MacLean and co-authors wrote in Nature Communications in May 2017, “Understanding causality in a quantum world may provide new resources for future quantum technologies as we gain control over increasingly complex quantum systems.” Inferring relationships of cause and effect, they stated, could provide quantum computers with a significant advantage over the most powerful computers now in use.

Cause and effect in a cascade of dominos. Image: Alicja, Pixabay
The connection between cause and effect can seem obvious for everyday events.
For example, if you cause a glass to drop to the floor, the effect is that the glass shatters. Cause-and-effect sequences are far less clear when we zoom in to the tiniest level of the quantum, but scientists are making progress in the hunt for the connections that could help unlock the power of quantum computing.
Probability is the culprit that can make cause and effect relationships difficult to determine, both in the visible physical world and in the invisible quantum realm. When a combination of many causes can generate an exponential growth of probable effects, how can we identify the order of events in time that gave rise to the outcomes?
In the observable physical world, randomized controlled trials are among the most reliable methods, involving experiments that isolate the effect of a specific variable by comparing two or more groups identical in all respects except for one manipulated factor. While randomized controlled trials help determine correlation, temporal sequence, and direction of causality among physical objects, there is no quantum equivalent.
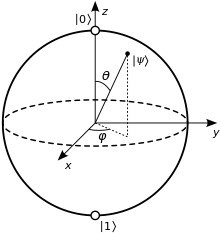
The qubit provides a spherical distribution of probabilities in the quantum computer. Signals are both on (denoted by “1”) and off (“0”) simultaneously. There is zero time difference between each state that comprises half the qubit, unlike today’s computer bits that require time to switch from one state to the other. Image of Bloch sphere: Wikipedia
Probability reigns in the quantum, which is the smallest amount of energy in the universe that can be either a cause or an effect of change.
The problem of probability is acute in quantum computing, because each quantum bit, or qubit, is in a “superposition” of opposite cause and effect states simultaneously. Qubits therefore operate entirely on the probability of outcome of one state or the other, or combinations of both.
Progress in tracking the order of cause and effect over time in quantum circuits is being made with the application of a method called “process matrix formalism.” The technique, which we will describe in more detail below, is designed to assess four different possible types of cause-and-effect relationships in quantum circuits. Process matrix formalism promises greater control over quantum processes.
Additionally, a particular type of circuitry used in quantum computing, called “tensor networks,” has recently been adapted for calculating probabilities of cause-and-effect interactions in turbulent fluids. It’s a task that has long defied even the most powerful supercomputers because of the vast arrays of combinations and permutations to analyze.
In fluids like water, gases, and air, turbulence produces an incredibly complex web of cause-and-effect relationships because more than two molecules interact at the same time. When millions of molecules are colliding and jostling each other, how can the tremendous number of probable effects be traced to individual causes?

Tracing sequences of cause and effect in fluid turbulence poses a tremendous computational challenge. Image: Leo, of Pixabay
Conquering probability with tensor networks, scientists have opened the door to possible future simulation of turbulent flows.
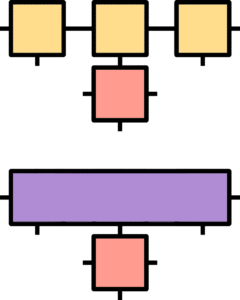
Illustration of two examples of tensor networks. Each is a single 7-indexed tensor and “the bottom one can be derived from the top one by performing contraction on the three 3-indexed tensors (in yellow) and merging them together.” Image and explanatrion by AtellK on Wikipedia.
The January 2025 paper Tensor networks enable the calculation of turbulence probability distributions, published in Science Advances, by Dr. Nikita Gourianov and co-authors, reports the new and far more finely-detailed extent of their ability to predict the dynamics of turbulent fluids.
“Even with modern computers,” they wrote, “anything beyond the simplest turbulent flows is too chaotic and multiscaled to be directly simulatable. An alternative is to treat turbulence probabilistically.”
Gourianov and co-authors approached the velocities and directions of fluid flows as if each change was a random variable, one that distributes throughout the fluid according to a statistical method known as “joint probability density functions” (PDFs).
They then applied the techniques of tensor networks to track the changing densities of variables and their combinations as they move through the fluid. Tensor networks are ways of making geometric connections between the magnitude (or scale) of probabilities, their speed, and their direction. This produces four measurement points – beginning of scale, end of scale, rate of change, and direction – to track a three-dimensional flow.
For a non-mathematician (like this writer), tensor networks are difficult to describe succinctly in words but perhaps more understandable by comparison to a flow of arrows (“vectors” in geometry and mathematics) through a fluid.
As they collide, the arrows can join in one of two ways. One way is by addition: when arrows add, they connect at a 90- degree angle so that one arrow is perpendicular to the other. The other is by multiplication, and when vectors multiply they join end-to-end in a straight line so that together they share a single beginning and a single end.
Tensors, vectors, and matrices are explained intuitively and graphically, using arrows, in this video.
Extending the metaphor to the work of Dr. Gourianov and research colleagues, they achieved a method of tracking sequences of cause and effect among a vast sea of arrows, in differing combinations that roll, surge, and subside against each other in the motion of a turbulent flow. They used tensor networks, which divide a flow into its components, so that they could pinpoint changes in the densities of bunches of arrows flowing in any direction.
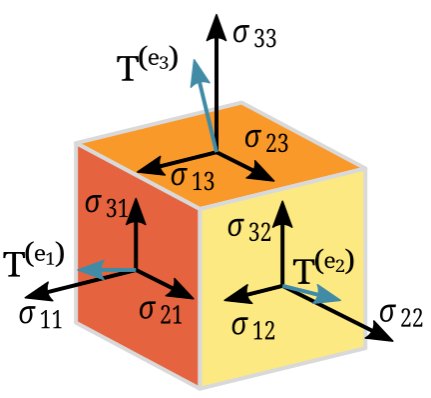
Illustration of second-order Cauchy stress tensor. The symbol “T” describes the stress experienced by a material at a given point, and the arrows represent vectors that indicate direction.
Tracing these changes in the flow backward in time, from effect to cause, the researchers were able to establish sequences of cause and effect in their correct order.
Understanding the correct ordering in time of cause and effect sequences in a turbulent flow, we could replicate the flow and produce a three-dimensional copy of its fluid motion.
In the summary of their paper, the researchers write that, “A future path is opened toward something heretofore thought infeasible: directly simulating high-dimensional PDFs [probability density functions] of both turbulent flows and other chaotic systems that can usefully be described probabilistically.”
Improved turbulence measurements and process matrix formalism share the goal of reducing probability.
Physicist Werner Heisenberg’s famous Uncertainty Principle, which applies universally, prevents us from obtaining a precise measurement of both the velocity and position of any quantum. Arranging quanta (the plural of quantum) in a matrix, however, allows for measurement of cause and effect among quanta moving in different spaces and at varying velocities.

The Uncertainty Principle says that the standard deviation from the mean (the symbol σ) of space (denoted as x), multiplied by the standard deviation of mass and velocity (denoted as p, which is momentum), is always either greater than or equal to the universal minimum – denoted by h (which is Planck’s constant), distributed to 2π (2π is a circle, and the bar through the h denotes circular distribution), and further divided into 2 equal halves.
While we can’t fully observe both position and momentum of an individual quantum, we can assess changes among quanta when they are arrayed in a series of matrices (the plural of matrix) that share the limits of a common neighbourhood. It’s a localized approach for probability reduction, with certain constraints, when there is no universal solution.
Quantum process matrix formalism measures the dynamics of quanta in matrices without making any assumptions about the order of cause and effect among them. The method allows assessment of all probable interactions, without giving rise to logical contradictions (such as “A comes before B but B comes before A”), regardless of the particular sequence of actions.

Children and adults of the 1970s became familiar with a matrix in the form of the Rubik’s Cube, a challenging puzzle requiring users to arrange cubes by their common colours. The Rubik’s Cube is separated into a matrix of 27 smaller component cubes, combined in three layers that can be rotated horizontally and vertically. Each of the Rubik’s Cube’s six faces is a different colour, consisting of three rows and columns of three cubes. The user can see either two or three colours on each of the 27 component cubes, depending on its position, and has to spin each of the three rows and columns of the matrix with the goal of matching colours on all 9 cubes of each face of the Rubik’s Cube. Image: Mike Gonzalez, on Wikipedia.
Process matrix formalism takes specific matrix arrangements in motion and translates them, in a mapping of their combined actions, to their net effect. The result can be compared to a tensor network, since both track changes in collections of probabilities as they evolve through time in a fluid-like motion.
As Dr. Emily Adlam, Assistant Professor of Physics who studies the philosophy of quantum mechanics at Chapman University, wrote in Is There Causation in Fundamental Physics? New Insights from Process Matrices and Quantum Causal Modelling, “The process matrix operates as a higher-order map from a set of quantum operations to another operation – i.e. it maps the quantum operations performed […] to an operation representing the net effect of performing all of those operations in the context of the particular process.”
Since the Uncertainty Principle ensures that we can only measure probabilities of quantum position and momentum in combination, quantum process matrices operate with four categories of possible cause-and-effect relationships between signals in a quantum computer.
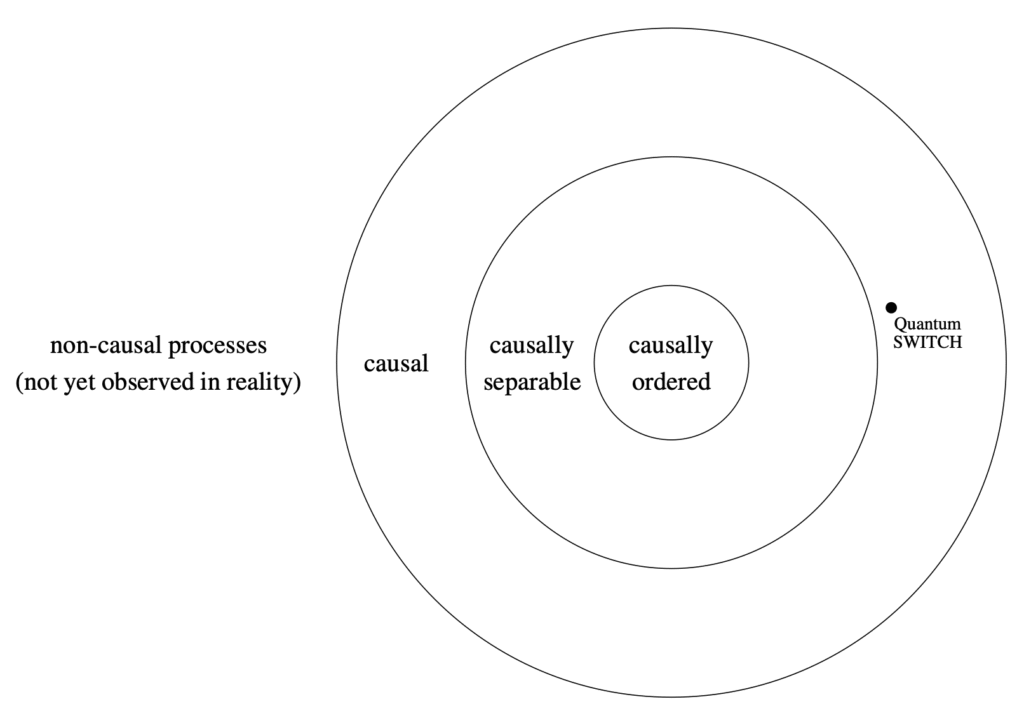
Diagram illustrating categories of probability relationships in process matrix formalism. “Quantum SWITCH” can be thought of as a branching of causal order, with multiple branches proceeding in different directions from a common root. Image: Emily Adlam, in “Is There Causation in Fundamental Physics? New Insights from Process Matrices and Quantum Causal Modelling.”
The first category, called “causally ordered,” produces a specific localized ordering, in a single direction, of cause and effect.
The second, called “causally separable,” decomposes the causal order of the first category into separately identifiable components. The third category is still causal, but is isolated from the first and can’t be decomposed like the second, and therefore has no effect on events that occur earlier in the sequential order. The fourth category, which is non-causal, isn’t found in the natural world where, according to Newton’s third law of motion, for every action there’s an equal and opposite reaction.
How much can probability be replaced by measurement certainty, with the help of tensor networks and process matrix formalism?
The question remains to be answered, but the potential for reduction of probability promises greater control over fragile circuits in quantum computers. The most significant roadblock to the implementation of fully-functioning quantum computers, and the speed and accuracy they promise that’s far in excess of the most powerful classical computers now in use, is the tendency of quantum circuits to “decohere,” or disconnect.
If scientists are provided a means to intervene in the signals that transmit from quantum to quantum, at precise positions and times, they could have far greater potential to decrease or eliminate the problem of decoherence.
The challenge of staging interventions in quantum circuits is a result not only of Heisenberg’s Uncertainty Principle, but also the quantum observer effect – the still mysterious phenomenon whereby the act of measurement changes the outcomes of quantum processes. How can simply looking at a quantum process, like a beam of light passing through two parallel slits, act as a cause and thereby produce a different effect? (For more on the observer effect, see our May 2024 article The Observer Effect: Why Do Our Observations Change Quantum Outcomes?)
While the Uncertainty Principle guarantees that we will never be able to eliminate quantum probability entirely, tensor networks and process matrix formalism are two relatively new tools that show great potential for circumventing the observer effect and delivering precision control to quantum circuitry.
With precision quantum control, the question that we could begin to ask is, “What are the probabilities for all the things we could do with the power of the quantum computer?”
The answer may be, “The sky is the limit.”
Craving more information? Check out these recommended TQR articles:
- Thinking in the Age of Machines: Global IQ Decline and the Rise of AI-Assisted Thinking
- Everything Has a Beginning and End, Right? Physicist Says No, With Profound Consequences for Measuring Quantum Interactions
- Cleaning the Mirror: Increasing Concerns Over Data Quality, Distortion, and Decision-Making
- Not a Straight Line: What Ancient DNA Is Teaching Us About Migration, Contact, and Being Human
- Digital Sovereignty: Cutting Dependence on Dominant Tech Companies




