
Image of the supermassive black hole called Sagittarius A* at the centre of the Milky Way Galaxy taken by the Event Horizon Telescope, with lines overlaid to show the orientation of its magnetic polarization. Released in March 2024, this image represents the first time that astronomers have been able to measure polarization, a signature of magnetic fields, at a distance close to the edge of Sagittarius A* and the black hole’s event horizon, where space and time end. Image: Event Horizon Telescope Collaboration
By James Myers and Mariana Meneses
What if Sir Roger Penrose is correct, that the measurements we make as conscious observers are imprinted in the fabric of space and time?
Would this help to resolve the puzzle of the quantum observer effect? The observer effect is the curious phenomenon we’ll describe in more detail shortly proving that light behaves differently when we observe it versus when it’s not observed. Light, like the quantum, is energy, and the obvious question is: why would a conscious observation affect energy?
The observer effect poses a significant problem to development of the quantum computer, and we’ll survey some of the latest thinking on the fundamentally challenging question of quantum measurement.
The science of measurement took a significant step forward when collaborators at the Event Horizon Telescope, which is an array of telescopes around the Earth observing the black hole at the centre of the Milky Way, succeeded in measuring the orientation of the magnetic poles surrounding the hole.
Polarity is the direction of electrical and magnetic flow and is ultimately positive or negative, like the two poles of the batteries we use in our electronic devices.
Measurement of magnetic polarity of the black hole that is about 27,000 light-years distant from Earth indicates similarities to its much larger cousin in the middle of the M87 galaxy. It also reveals “that strong and ordered magnetic fields are critical to how black holes interact with the gas and matter around them,” according to Sara Issaoun from the Harvard & Smithsonian Center for Astrophysics and co-lead of the project that imaged the polarization of the hot gases swirling around the black hole.
Black holes attract and eject gases and physical matter with such force that they have a profound effect on the shapes and compositions of galaxies, astrophysicist Caleb Scharf wrote in “Gravity’s Engines: How Bubble-Blowing Black Holes Rule Galaxies, Stars, and Life in the Cosmos.” Knowledge of the magnetic polarities around the Milky Way’s central black hole could tell us much about the past and future of our galaxy.
Now that a crucial feature of the black hole has been measured, is there a permanent record somewhere in the universe of that measurement?
Roger Penrose’s answer would seem to be “yes.”
Penrose received the Nobel Prize in 2020 for assembling the mathematical tools that are required to measure black holes, those mysterious objects that inhabit the centre of all galaxies including our Milky Way and are millions of times more massive than the Sun. Since black holes aren’t composed of either space or time – the event horizon of a black hole is where space and time end – they can be measured only by their gravitational, electromagnetic, and other effects on physical objects like planets and stars that surround them.
Penrose proposed that each conscious measurement by observers like you and me is preserved, or recorded, with a unique position in the curvature of space and time. The idea, which is not yet widely accepted, is that the fabric of the universe acts as a storage device for our memories, recording conscious information for all time in the energy and mass that surrounds us.
If Penrose is correct, could the imprinting of observational information in the same spacetime structure that is simultaneously being observed cause a change in physical outcomes such as we see in the observer effect? Or is it possible that the imprinting process, if it occurs, would be of no consequence to either space or time?
Conscious measurements are information and are subject to the universal law of conservation of information.
The problem of the observer effect arises because the information of our observations is recorded in the same medium – the fabric of spacetime – that constitutes the physical objects that we observe. It would be as if storing data on the hard drive of your computer warps the hard drive itself, causing the sequences of data originally recorded on it to change.
How could the hard drive retain an accurate account of data sequences, if the mere act of recording more data changes the entire dataset that preceded it?

Artistic representation of the fabric of spacetime showing its curvature around a massive object such as the Earth. Roger Penrose proposed that conscious observations are recorded in spacetime curvature. Image: Mysid
To the extent that our conscious measurements are information, Penrose’s idea has a logical basis in the universal law of conservation of information.
The law says that information can neither be created nor destroyed but is preserved in the universe because it has nowhere else to come from or go to. The law of conservation of information was hotly debated between physicists Stephen Hawking, who established that black holes evaporate over a very long time in a process now called Hawking radiation, and Leonard Susskind. The debate was settled by the proposition that information falling into a black hole is recorded in its event horizon, as if the data are preserved in a two-dimensional holograph around an object occupying three dimensions.
Since quantum measurement changes the outcome of the thing that’s being measured, it is very different from essential everyday measurement.
What consequences would emerge if observational information were imprinted in quantum curvature?
The phenomenon known as the quantum observer effect makes measurement a fundamental problem for us at the level of the quantum, which is the basis of the quantum computer and the tiniest amount of energy in the universe that can either cause change or be changed.
At a much higher level, however, the ability to measure is essential to our daily survival. As conscious beings, we use our senses to measure the physical objects that surround us every waking moment, almost unthinkingly. Imagine what it would be like if you had no measurement data at all from any of the five senses: no seeing, hearing, tasting, touching, and smelling. How could you exist in the physical world without knowing where you are in space and time, which objects are greater or lesser than you, and the distance and speed required to get from wherever you are to wherever you either need or want to be?
Are the mathematical symmetries that exist in the constants of the physical universe also represented in conscious information?
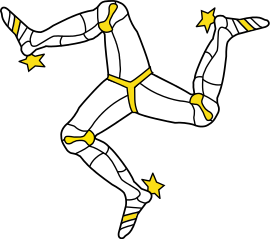
The triskelion, which appears on the flag of the Isle of Man, is a shape that has three-fold rotational symmetry, meaning that it appears the same when rotated by one third of a full turn about its centre. Because its appearance is identical in three distinct orientations, its rotational symmetry is three-fold. (Image: Wikipedia
If Penrose is right that a conscious observation is recorded in the curvature of spacetime, would that necessarily mean that human consciousness and the physical universe exist in a symmetry of two distinct sets of information? Symmetry would ensure that conscious information equals physical information and vice-versa, with neither form of information being able to outrun the other in space or time.

Mathematician Emmy Noether, c. 1930. Image: Wikipedia
The wondrous thing about symmetry, as we earlier highlighted the work of mathematician Emmy Noether – who Einstein hailed as brilliant – is that for every physical constant like the speed of light or the force of gravity there is a mathematical symmetry.
A symmetry is when equal halves agree, and in their agreement they can be measured to two equal extremes from a single point only. The single measurement point for two equal extremes is at their combined middle, because the middle is not part of either extreme. There is no interference in the middle.
Since the observation and that which is physically observed exist simultaneously as information in the same medium of spacetime, their mathematical symmetry would ensure no unaccounted differences between them. Symmetry would also ensure that both types of information can co-exist without external limits and with zero friction and resistance. Each information stream would retain complete fidelity to its individually-established sequences in space and time.
As observers, we might be grateful if this were true, because then the potential power of our measurements could never be weakened by anything physical. It would also mean for us no loss of conscious fidelity as we make our way through space and time, and the ability to retrieve information instantly with no time delay required for reflection. 
If mathematical symmetry prevails the same way in our conscious observation as it does in all the physical things we observe, it might go a long way to explaining the quantum observer effect.
Is the centuries-old problem of the quantum observer effect close to resolution?
Two centuries ago, Thomas Young proved that the behaviour of light, which we now know defines the universal speed limit in time, depends on whether quantum energy is observed or not observed. (The distance light travels in time is the “c” in Einstein’s immortal equation E=mc(1+1) that even children now know).
The quantum observer effect poses a most curious and deeply puzzling question that has defied science in the 223 years since Thomas Young’s famous experiment in 1801. It continues to defy those who are developing quantum computers which operate by connecting computing inputs and outputs to the quantum.

1822 portrait of Thomas Young by H.P. Briggs. Image: Wikipedia
How can observation affect anything physical? That’s the natural question anyone would ask, when it’s plain to see that we can’t bend spoons with our very thought power. (At least most of us can’t bend spoons, although mentalist the Amazing Kreskin demonstrated a power like that in the 1970s!)
The quantum observer effect and Thomas Young’s 1801 experiment are brilliantly demonstrated by Derek Muller, a physicist and science communicator known, among other works, for his YouTube channel Veritasium, which has gathered over 15 million subscribers to date. In the video below, he recreated Young’s double-slit experiment with sunlight in a public setting, inviting passersby to pose hypotheses about how light would behave in a large box with two very narrow slits. He then invited them to observe—and be astonished by—the outcome.
Looking into the box, they saw two beams of light interfering with each other forming a line of numerous dots, with the middle dot appearing whiter and a rainbow-like spectrum of colors in different wavelengths as the light spreads out to two extremes. Muller explains the complexities of the interference pattern and colour distribution so clearly that the participants in his experiment were both astonished and fascinated.
The Original Double Slit Experiment | Veritasium
Recall that the quantum, which is the basis for new and very powerful computing technology, is the minimum unit of energy (the E in Einstein’s famous equation) that can either cause change or be the effect of change.
In our conscious measurements of time, we are measuring cause and effects and their logical connections, to understand the order of time: what event came first, what event occurred second, and so on.

Albert Einstein’s portrait for the 1921 Nobel Prize in Physics. Image: Wikipedia
Another way to think of the observer effect might be this: within the infinite realm of probabilities for the paths light might take (because there’s nothing in the universe that can outrun light), there are only so many combinations that light can take when it connects to itself observably. Observable things exist in three dimensions of length, width, and depth (that we call space) and two extremes of time (that we call beginning and end). When energy connects to itself from beginning to end in this way, it has “resistance”, which is the word physicists use for “mass” – which is the “m” in Einstein’s famous equation. We can only measure physical “things” because physical “things” have mass, and our five senses are tuned to detect mass.
Our consciousness, however, is tuned to measure both mass and things without mass – massless things like ideas and emotions. Massless measurements seem to be a fundamental basis of our imaginations, for our ability to see both what is not and what is, and therefore act on our calculations of what might be.
Mathematical symmetry relates directly to physical constants.
Our instruments for measuring physical symmetries are becoming highly advanced and sensitive. At the end of 2022, The Quantum Record explored Laser Interferometer Gravitational-Wave Observation (LIGO) technology, wondering if it might conquer the a century-long quest to detect physical memory in spacetime. LIGO consists of a long series of mirrors so finely tuned that they can measure the slightest vibrations in the fabric of spacetime caused, for example, by the collision of stars millions of light-years away from us.
At the beginning of this year we described the work of Dr. Andrew Stromminger and colleagues who proposed that a black hole’s photon ring has the kind of symmetry that often arises in a hologram. In August 2023 we reported on the observation by Jeff Hazboun of a universally pervasive low-frequency vibration, asking whether it might be an indication that the universe has a holographic memory.
Early last year, The Quantum Record asked, What’s in the Middle of Black Holes and Why Do We Care? and we have now come full circle back to the question. If we can now measure the extent in spacetime of the nothingness that’s occupied by a black hole, can we equally measure the opposite of nothingness, meaning every physical thing?
Now that the questions are on the table, what do they say about the quantum observer effect and the recording of our conscious memories in the curvature of space and time as Roger Penrose proposed?
Part of Penrose’s proposition is that when conscious observations “entangle” or connect with the quantum, and when successive entanglements become separated by more than one Planck length, the result is a collapse of the quantum wavefunction. The Planck length is the universal minimum length of a unit of energy, and the quantum wavefunction oscillates in Planck length increments between multiple states in space and time. The wavefunction collapse would therefore fix an “observation” by imprinting it at one specific point in spacetime.
How does this proposal relate to the mechanics of the quantum observer effect?
Let’s return to Derek Muller’s recreation of Thomas Young’s discovery of the quantum observer effect and what has become known since then.

Image generated using Ideogram Ai.
The double-slit experiment, renowned in physics, demonstrates the dual nature of light as both a particle and wave.
Picture a scenario where light from a laser is directed at a wall with two closely positioned thin slits, facing another wall which captures the light passing through the slits. A common expectation is that if light exhibits only particle-like behaviour, as if the laser beam consists of minuscule projectiles, two distinct lines of light would emerge from the slits and project an outline of each slit on the facing wall.
Something unexpected happens, as the participants in Derek Muller’s experiment experienced, when the path of the light is observed. The act of observation causes the projection of the beam through the two slits to create a different pattern on the facing wall than the same beam creates when it’s not observed.
Observation, in which the light’s path is measured, results in an interference pattern on the facing wall somewhat like overlapping ripples in water when two stones are cast at the same time into a tranquil pond, indicating a wave-like behavior instead of individual particles. Intriguingly, this pattern persists even when the observed light travels through the slits one particle at a time, implying a baffling scenario where each particle seemingly traverses both slits simultaneously, interacting with itself in the process.
Originating with Thomas Young’s exploration of the wave-like nature of light in 1801, which challenged the theory of Isaac Newton that energy consists of only particles, the double-slit experiment has been replicated with electrons, atoms, and molecules. The result consistently demonstrates the wave-particle duality inherent in light, whose photons are the smallest, fundamental units of electromagnetic energy.
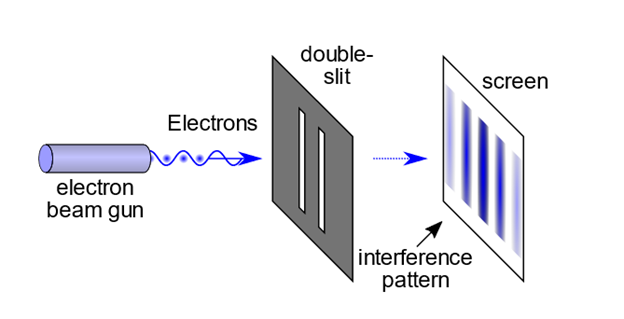
Double-slit experiment – interference pattern. Image: Wikimedia
Thomas Young’s experiment was designed to demonstrate the wave behaviour of light.
In the 223 years since it has become a pivotal demonstration of the observer effect in quantum mechanics. In the experiment, particles (or photons) of light exhibit both particle-like and wave-like behavior: the former if their path over time is observed, and the latter if only their final position in space on the screen is observed.
When their motion through space and time is unobserved, light photons behave as waves, simultaneously passing through both slits and joining to form an interference pattern on the detection screen. However, when the path of the photons is observed from beginning to end, they behave as discrete particles, passing through one slit or the other, without creating an interference pattern.
This phenomenon illustrates that the act of observation itself influences the behavior of quantum particles, suggesting that the observer plays a crucial role in determining the outcome of the experiment. The observer effect implies that the very act of measuring a quantum system by observation can alter its behavior, challenging our classical intuition that what appears to be “reality” is independent of the observer’s mind.
Instead, it appears that the measurements we make with our observing minds are intrinsic and consequential to reality.

Image generated using Ideogram AI.
Quasi-probabilities
In their recent research article, K. Onggadinata, from the Centre for Quantum Technologies at the National University of Singapore, and team (2024) propose a novel approach to resolving the quantum observer effect.
They are exploring the use of “quasi-probabilities,” which are probabilities that can assume negative values, to describe and understand the observer effect. This departure from traditional probability theory allows for a more nuanced understanding of the observer’s role in quantum phenomena. Their study delves into the concept of Specker’s triangle scenario, a fascinating experiment comprising three observables represented by boxes, each potentially containing a hidden ball.
The counterintuitive behaviour emerges when regardless of the pair of boxes chosen for simultaneous measurement, one box inevitably contains the ball.
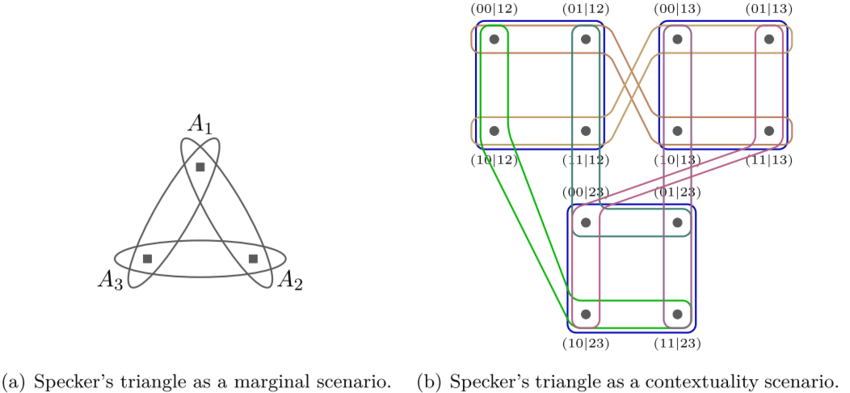
Illustration of Specker’s triangle: “(a) Hypergraph representation of its formulation as a marginal scenario. Each vertex denotes a measurement, and each hyperedge a context. There are three dichotomic measurements which are pairwise compatible. (b) The events-based representation of the same scenario. The vertices are given by the events. The Specker’s triangle corresponds to a (3, 2) symmetric marginal scenario.” Image from Gonda, Tomáš & Kunjwal, Ravi & Schmid, David & Wolfe, Elie & Sainz, Ana. (2017). Almost Quantum Correlations are Inconsistent with Specker’s Principle. Quantum. 2. 10.22331/q-2018-08-27-87.
This scenario not only illustrates the peculiarities of quantum systems but also underscores the profound effect of observation on their behaviour.
Expanding on this scenario by including additional boxes and multiple balls, the researchers demonstrate how negative probabilities can amplify the observer effect. This perspective provides valuable insights into the complex interplay between observation and quantum phenomena, offering new avenues for theoretical exploration and practical applications in quantum information science and beyond.
The quantum observer effect gives us each a unique power.
- Can the information collected by a satellite about the past of the universe still be obtained by someone else in the future?
- What part of the information is consumed and changed, after it is collected?
- Is the reason we see what we do about the world due to the fact that no one else has seen it from the exact spacetime position before?
- If so, does this imply that what you and I have discovered has not been uncovered in the same way by another intelligent being in the universe?
- Do all individual pieces of information observed by one individual form part of that observer?
- Does the information we collect become a part of us, not destroyed but transformed as it deviates from its previous trajectory?
Is the information connected or attracted something, such as our satellites and ourselves, as we learn by consuming the information?
If you and I and every other observer is fundamentally unique – meaning that we are each a specific collection and distribution of atoms and molecules with a history of positions in space and time like no other, and cannot share positions with another pair of eyes – is all the information we consume, which is influenced by who and where we are, forever inaccessible to others?

What are the causes and consequences of the way you observe the world? Image: baruani2020 via Ideogram AI
Craving more information? Check out these recommended TQR articles:
- Science Probes the Frontiers of Quantum and Mathematical Consciousness
- The Science of Consciousness: Have We Finally Solved the Mystery Inside Our Heads?
- The Geometry of Information: Is Topological Quantum Computing the Future?
- Remembering or Forgetting? Quantum Computing May Need Both
- Quantum Sensing’s Revolutionary Potential for Cancer Treatment, Navigation, and Precision Measurement
- The Future of Quantum Computing Accelerates, Many Qubits at a Time
- Building Future Scientists: Girls in Quantum and the Quantum Qid Foundation




This is my first time on your site. I am surprised and amazed by the information supplied in an understandable format. I originally thought it would be in some mumbojumbo scientific jargon that I could never decifer as a layman. But I was pleasantly surprised to find the article was layed out in an understandable terminology that even I with limited scientific knowledge could understand. A great article indeed. I will be returning, as time permits, to peruse more of your site. Thank you for writing articles that an old man like me can enjoy and learn from.