
Forgetting is not simply failing to remember; it has its own purpose too. Image: Freepik
By Mariana Meneses
Non-Abelian anyons are a fascinating feature in the world of quantum physics, and may provide the key to error-free quantum computing.
Anyons are a type of quasiparticle that exists only in two-dimensional systems.
Unlike conventional particles, such as protons and electrons, anyons exhibit neither attractive nor repulsive forces when changing positions. Instead, and intriguingly, they leave behind a trace of their wavefunction as they move. Drawing an analogy to Carl Sagan’s Flatland, where inhabitants exist in a two-dimensional world, one can envision anyons as exotic entities navigating this flattened realm, distinctly marking their paths during interchanges.
Let’s think of non-Abelian anyons as if they were books in a library.
In a normal library, if you swap the positions of two books, nothing really changes. The library is still the same. But imagine a magical library where the books are non-Abelian anyons. In this library, if you swap two books, the entire library subtly changes.
The change depends on the order in which you swapped the books.
If you swap book A with book B and then with book C, the library would provide different information than if you swapped book A with book C and then with book B. This is similar to how non-Abelian anyons behave. They remember the order in which they were swapped, and this “memory” could potentially be used to store and process information in quantum computers.
The idea is that by braiding non-Abelian anyons, quantum computations can be performed in a way that is inherently resistant to errors. This is because the information is stored in the global properties of the system, which are not subject to local disruptions from heat, electromagnetism, or other sources.
And progress is being made.
As reported by Quanta Magazine, physicists have achieved a groundbreaking milestone by successfully creating and manipulating non-Abelian anyons.
Utilizing quantum processors, researchers from Quantinuum and Google demonstrated the braiding of these non-Abelian anyons, which is an essential process for storing and manipulating information in quantum computers. The achievement represents a significant step towards developing error-tolerant quantum computers, as non-Abelian anyons possess nearly indestructible records of their journeys through space and time.
The experiments highlight the potential of quantum processors to advance the understanding and application of topological quantum computing.
The ability of these quasiparticles to remember may help us in the direction of the quantum computing future. However, just like in our everyday lives, quantum computing can also benefit from the ability to forget.
As highlighted by Dr. Scott A. Small, of Columbia University, forgetting is not merely a failure to recall information, but an active process that aids the brain in making decisions more efficiently. It helps us prioritize, think better, make decisions, and be more creative. Forgetting allows us to discard irrelevant details, preventing them from interfering with new learning or ideas.
And quantum algorithms might also benefit from this ability.
As reported by Quanta Magazine, quantum maze-solving algorithms, utilizing the principles of quantum physics, can navigate mazes exponentially faster than classical algorithms. However, a trade-off exists, as these quantum algorithms forget the paths taken to reach the exit.
Recent research, led by Matthew Coudron and colleagues, demonstrates that this trade-off may be inevitable for a broad class of fast quantum algorithms, specifically those dealing with a maze structure called a welded tree graph. The study suggests that any quantum path-finding algorithm avoiding blind guessing would need to temporarily lose track of the entrance.
Despite the fast quantum speedup, the algorithmic forgetting raises intriguing questions about the limitations and trade-offs inherent in quantum maze-solving approaches.
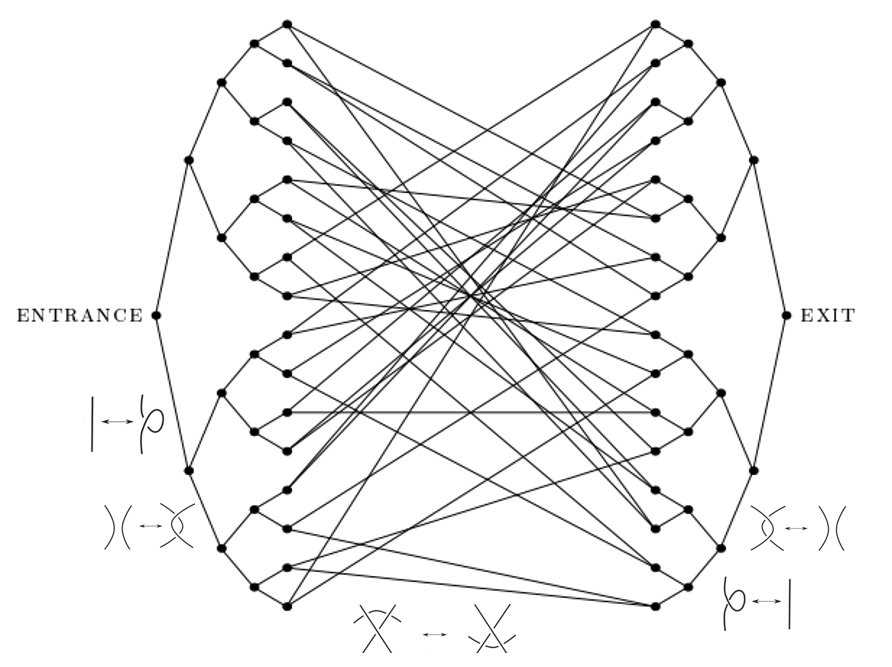
Welded tree graph. Source: Stackexchange .
A welded tree graph is a specific type of mathematical structure used in the field of quantum computing that can be thought of as a maze. It is used to study quantum walks, a fundamental tool in quantum algorithm design. Quantum walks are like random walks in quantum computing, where a particle can move in multiple directions at the same time due to quantum superposition.
In the realm of quantum computing, the interplay between the enduring memory of non-Abelian anyons and the strategic forgetfulness of quantum maze-solving algorithms not only signifies progress in error-tolerant quantum computation but also hints at a future when harnessing the dual capabilities of remembering and forgetting may unlock unprecedented efficiency and creative problem-solving potential.
Let this be a reminder that, sometimes, holding onto things is crucial, but at other times, letting go a little can make things work better.
Interested in exploring related topics? Discover these recommended TQR articles:
Breakthrough in Error Correction Opens Potential for Large-Scale Quantum Computer Processing
The Future of Quantum Computing Accelerates, Many Qubits at a Time
One-dimensional metal may provide the perfect on/off switch for quantum devices
Beyond the Binary: Can Machines Achieve Conscious Understanding?



