
A stone skips across the water. Imagine the task of a topological quantum computer as tracking the ripples of each stone hitting the water and their combinations with the waves of stones that hit the water earlier. Image: Wikipedia
By James Myers
Topological quantum computing is a theoretical form of computing proposed in 1997 by physicist Alexei Kitaev that holds promise to overcome error correction challenges in today’s quantum computers.
Research is advancing the goal of realizing the speed and accuracy of quantum computing using the geometry, or topology, of quantum signals and mapping the shape of the signal phases over time.
A phase refers to a signal’s shape, or angle from the signal’s beginning to its end, at any single point in time. Think of the quantum signal’s angle like an arrow, its pointed end shooting in a particular direction in three dimensions. Over time, as the arrow combines with other signals transmitting around the system at differing angles, the phase of the quantum signal shifts: the signal maintains its unique angle, but its arrow points in another direction – like a single wave washing through a turbulent sea of many crashing waves.
Imagine drawing the topology of quantum signals as if you’re skipping stones across the surface of a pond, making a record of the ripples of each stone hitting the water and combining with the waves made by the stones that you threw previously.
If you could draw the combinations of waves from your skipping stones, their intersections would form a graph, and graphs are essential to describing quantum circuits, as R. Manenti and M. Motta point out in their new text, Quantum Information Science. A graph, like a map, consists of nodes (on the map, these would be towns) and edges connecting the nodes (like roads running between towns on the map).
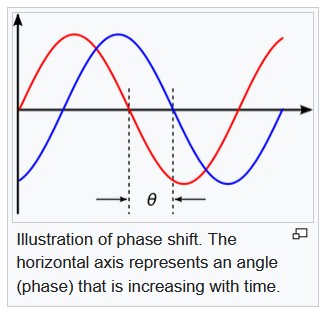
Illustration of change, or shift, between two signal waves. Image: Wikipedia.
Tracking so many intersecting phases, however, would be an impossible task for the human eye, but mathematical tools could make the task possible at the tiniest level of the quantum.
Accurately mapping the continuous geometry of quantum signal limits over time could result in a significant reduction of connection errors that plague today’s quantum computers.
Practical and powerful quantum computing applications would most probably follow, when signals can connect without error over an extended time. Particularly important, perhaps, is that we could trace the graphs of quantum signals with a high degree of probability of visiting every node (which is called the Hamiltonian path) and tracing every edge (referred to as the Eulerean path) only once.
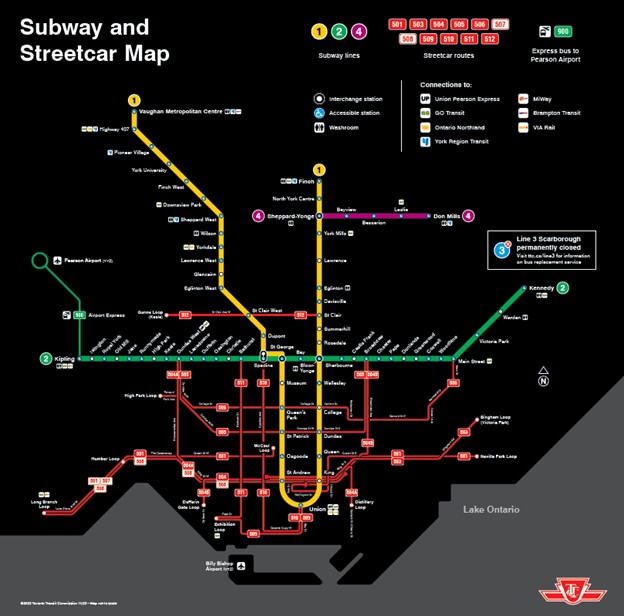
A transit map, like the City of Toronto’s, could be called a graph. Stations would be nodes and the different-coloured lines would be edges. Image: Toronto Transit Commission
What’s the definition of “quantum” and how is it used in the computer?
The quantum carries physical information. The quantum is the smallest unit of energy in the universe that can either cause a change in physical mass or be changed physically. Being the smallest unit, the quantum’s energy necessarily contributes to every greater quantity of energy, to the universal extent of E=mc(1+1) according to Einstein’s famous equation.
The quantum “is” neither cause nor effect, but at all times “is either.” As energy compresses in space and gains gravitational resistance, it forms physical mass (the m, on the right-hand side of Einstein’s equation), and Newton’s second law of motion says that with all physical mass, for every action (as a cause) there’s an equal and opposite reaction (as the effect).
The problem with the second law of motion is that it leaves no difference in mass when all actions and reactions are added together in space and time.
Think of an action like a negative number, that subtracts from the whole, and the reaction as a positive number that returns to the whole what was taken away: negative and positive combine to zero. But physical existence requires differences in energy, and those differences reach their limits in the shape – which is boundary, or the limit – of the physical thing. All quanta having, as a whole, zero difference, the question for the existence of a particular physical object then becomes one of setting limits, with a unique combination of quantum cause and effect in energy that makes “the thing” different from “all other things.”
“Shape is the limit of a solid” – Socrates, in Plato’s Meno (76a)
Think back to the pond with the skipping stones. If each drop of water displaced by a stone as it hits the water’s surface is like a physical thing, then each splash is a differently-shaped physical thing as the stone loses momentum and changes direction before, after a time, it sinks.
Setting Limits in the Topological Map of the Quantum Computer
Although in general one quantum is like any other quantum, which makes them difficult to graph, a particular combination of quanta (the plural of quantum) makes up the energy that defines the beginning and end of each physical object. A physical object (like a table) differs in shape from another physical object (like a chair) because there’s a different combination of energy that makes up the limits – which we call the shape – of each of them.
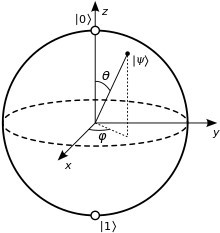
The qubit provides a spherical distribution of probabilities in the quantum computer, where signals are both on (denoted by “1”) and off (denoted by “0”) simultaneously. There is zero time difference between each state that comprises half the qubit, unlike today’s computer bits that require time to switch from one state to the other. Image of Bloch sphere: Wikipedia
Our definitions for physical objects according to their shapes is intrinsically connected with the energy required to compose any form of that physical object.
Signals in the quantum computer transmit the probability of cause or effect in the qubit, which is analogous to the binary bit used in today’s computers. Unlike the linear computer bit, however, the spherical geometry of a qubit can contain an unlimited range of probabilities, making the qubit particularly susceptible to measurement errors.
Qubits operate in entangled pairs, such that what happens in one qubit instantly occurs in its connected partner without the passage of time. You might think of a topological quantum computer’s work as constructing a signal map among spherical qubits. The map begins in two dimensions (of length and width), which are then projected to probable changes in four dimensions (consisting of the length, width, depth, and time that we live in), and finally recorded in three dimensions (of length, width, and time).
Signal mapping has been particularly difficult in existing quantum computers, and the properties of quantum mechanics pose a significant challenge to measurement and memory.
Further complicating matters is that existing quantum computers have been severely limited by the instability of their connections, which suffer from the accumulation of external interference, or “noise,” of electromagnetic signals, heat, and other disruptions. This noise can cause qubits to disconnect, resulting in localized errors in memory from the “decoherence” of quantum signals.
However, small disturbances would not change the signal maps in topological quantum computing, although error correction methods would still be required.
As explained by University of Wisconsin-Madison physics PhD student Ryan Simeon (in a paper posted in pdf),
“In a topological quantum computer, rather than encoding the information locally, information is encoded more globally, involving topological properties of a multi-quasiparticle system. By topological properties, I mean those that are invariant under “bending” and “stretching”, so that local perturbations do not change the encoded information.”
The quasiparticles that Simeon refers to are anyons, which are two-dimensional particles discussed in TQR’s January 2024 article, “Remembering or Forgetting? Quantum Computing May Need Both.”
Anyons may provide the key to stable quantum computing memory by causing zero resistance in their transmission but leaving a measurable record of their changes over time. Since quantum signals cannot be replicated, non-Abelian anyons could be particularly important by providing non-commutative pairings in signal groups such that changing the order of the operation of connected qubits does not produce the same output.
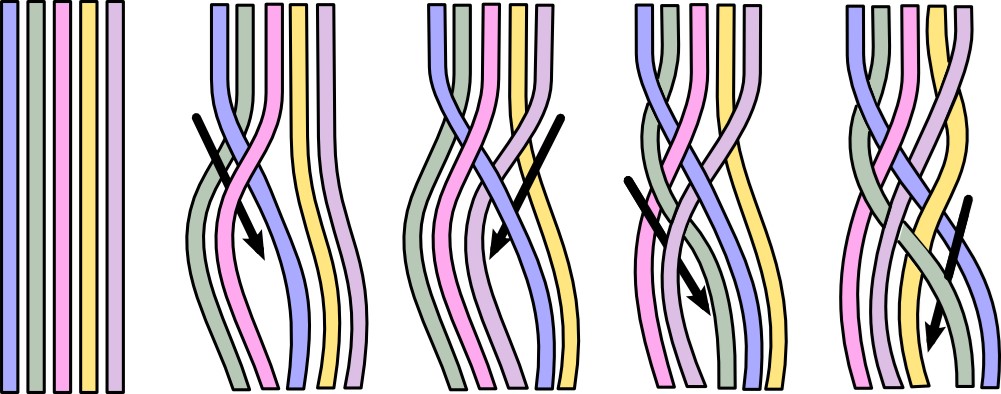
Measurement of quantum phase changes is represented in the three-dimensional braiding of quantum signal topology. image: Wikipedia
Topological quantum computers record the evolution of anyon paths mathematically in 3-dimensional “braids” that are defined by two spatial dimensions and a single dimension of time.
The relative orientation of the braids is their “topology,” which you might think of as the shape and direction of the signals that the braids carry, perhaps like a railway hub with trains arriving and leaving on multiple tracks. The crossings of the braids would constitute the quantum computer’s logical gates, where one or more binary inputs are transformed into a single binary output indicating whether, for example, the inputs are false (“NOT”), all true (“AND”), or partially true (“OR”).
The theoretical advantage of topological quantum computing over existing methods is the stability of the topological braids and their logical gates.
Although topological quantum computers would still require error correction methods, one suggestion is that increasing the distance between the two-dimensional anyons would provide sufficient adjustment. There has also been discussion of the use of Fibonacci anyon models, in which the number of quantum states grows like the Fibonacci sequence (that is, 0, 1, 1, 2, 3, 5, 8, 13, 21, etc. states) such that nearest-neighbour pairings of anyons would provide information on the accumulation of the entire system.
Photonics and Topological Quantum Computing
Photons are massless particles of light, and research is advancing the possibility for qubits based on photons to replace error-prone trapped qubits. As Manenti and Motta explain, “Photons propagate along waveguides in integrated circuits and are manipulated with non-linear optical elements.” Over time, the bended light waves trace a graph.
The challenge is to protect the topology of light (from sources like lasers), so that the light’s path is not subject to interference in its geometry and shape as it transmits through circuits over time.
In an April, 2021 paper “Quantum Topological Photonics,” Quichen Yan from the Beijing Academy of Quantum Information Sciences and co-authors outline the new research field and its potential as the stability of quantum light sources improves the ability to graph phase shifts in the topology of quantum signals. The potential for topological research in quantum phenomena was recognized when the 2016 Nobel Prize in physics was awarded for theoretical discoveries of topological phase transitions and topological phases of matter.
Xanadu is a Toronto-based company that aims to create a million-qubit fault-tolerant quantum computer with photonic qubits, when IBM shares the current record with 1,121 entangled qubits in its Condor system announced in December, 2023. Xanadu’s video demonstration explains how this could be possible within the decade using existing photonic manufacturing techniques.
What will shape the future of quantum computing?
We are coming closer to the answer, with the help of mathematical and geometric methods like topology and braiding that could provide a fundamental paradigm shift in the approach to realizing the unimaginable speed and accuracy of quantum computing.



