
String theory posits that everything in the universe operates with strings of energy that vibrate at differing frequencies that can be measured by their colour. Illustration by dp792 on Pixabay.
By James Myers
Physicists like Harvard University Professor Andrew Strominger are working to solve problems that include the unification of forces and particles and the quantum structure of a black hole and its boundary. Underlying much of this work is string theory, which is the idea that everything in the universe operates with tiny strings of energy that vibrate at different frequencies.
Among Dr. Strominger’s accomplishments was the discovery of what are called Calabi-Yau compactifications, which, as he states, “demonstrated that string theory not only reconciles quantum mechanics and gravity but can also contain within it electrons, protons, photons, and all the other observed particles and forces, and hence is a viable candidate for a complete unified theory of nature.”

Dr. Andrew Strominger. Image: Perimeter Institute
Working with calculations from the 1930s by Felix Block and Arnold Nordsiek, Dr. Strominger has defined the properties of a universal process called “supertranslation.” First identified in 1962, a supertranslation is an infinite-dimensional extension of the memory of gravitational changes that arise from the interactions of particles. These changes can be as tiny as those of the quantum at the universe’s minimum scale, all the way to the gravitational actions of stars at the universe’s maximum scale.
The Block-Nordsiek calculations of nearly a century ago establish that in the collision of two “soft particles,” which are zero-energy photons (photons are massless particles of light), the probable outcome of any interaction is independent of the number of particles produced from the collision.
In simpler terms, the effect of this independence of probabilities is that, at low energy, all particles work the same way.
Dr. Strominger’s work has led to an understanding that, because of supertranslations, soft particles are added to the fabric of spacetime, with each soft particle preserving memory of the gravitational consequences of its collisions. Although the soft particles add no energy to the system, they contribute their angular momentum, which shapes the system’s boundaries. As a result, while gravity weakens as distance from a massive object increases, it never completely disappears, even at infinite distance, because its effects are preserved in the curves of the spacetime boundary.
Soft particles could determine the shape of the vacuum of outer space. As science writer George Musser observes in How the Universe Remembers Information, republished in The Nautilus, “Plop a soft particle into a vacuum, and though it adds no energy, it does contribute its angular momentum and other properties, thereby bumping the vacuum to a new version of itself. Strominger realized that if the vacuum can assume multiple forms, it will retain an almost homeopathic imprint of what passes through it.”
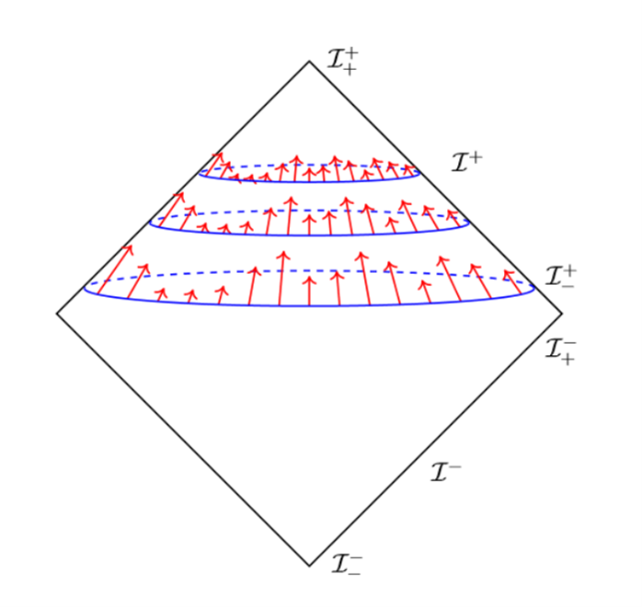
Representation of supertranslation, imprinted in the direction of the red arrows, of information in the curved blue lines, to future infinity (I++). Image: BMS Superrotation and Supertranslation (A Review of Strominger’s Work) by Lim Zheng Liang.
Supertranslations ensure that the fabric of spacetime doesn’t completely flatten but always retains some degree of curvature and bending that imprint in their geometry the gravitational memory of soft particles.
In 2014, Dr. Strominger realized that two formulas, one published in 1965 and the other 20 years later, established that the effects of collisions of tiny, elementary particles are calculated the same way as the outcomes of colliding supergiant black holes and stars. In quantum memory storage, this could mean that records of quantum interactions of any extent—from the smallest objects to the largest—might be efficiently recorded using the same algorithm and stored in the same way.
If there is a universal quantum memory, in supertranslations or otherwise, how do we decode it?

Princeton University doctoral candidate Carolina Figueiredo. Image: Princeton University.
Remarkably, interactions of particles are proving to be similar in their outcomes. In 2022, Princeton University PhD candidate in physics Carolina Figueiredo calculated the consequences of collisions involving three different types of subatomic particles and found no difference between them. She and her colleagues theorized that this is evidence of an underlying geometric structure that operates at the most fundamental level of reality.
The discovery advances an emerging geometric method, called “surfaceology,” that may allow tracking of probabilities of quantum events without the painstaking and error-prone work of diagramming vast numbers of interactions among particles. There are many possible outcomes when quantum particles collide, including their merging into one, splitting into many, or a combination of both. Some think the surfaceology method could eliminate the need to analyze the myriads of outcomes moving through the fabric of spacetime, allowing instead a focus on their foundational geometry.
Surfaceology replaces intricate diagrams of trajectories of many particle interactions (called Feynman diagrams, after their creator, Nobel laureate Richard Feynman) with curves in differing arrangements. Quanta Magazine quotes Brown University physicist Marcus Spradlin, who said that with surfaceology, “There’s an exponential compactification in information.”
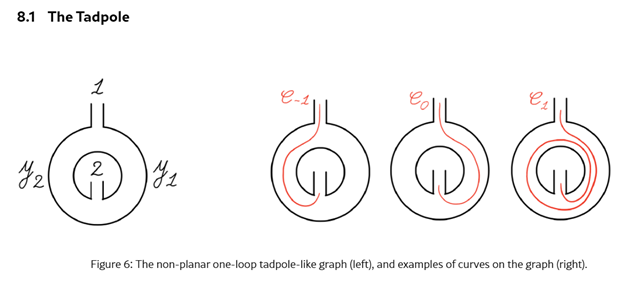
This example of curve analysis in a configuration reminiscent of a tadpole is from a paper entitled All Loop Scattering for All Multiplicity, published this September by Carolina Figueiredo’s doctoral supervisor, Dr. Nina Arkani-Hamed, and co-authors.
Encoded in the curves of surfaceology are the orientations and numbers of particles involved in an interaction.
When the momentum of particles before and after an interaction is known, the curves can be represented in three dimensions in which the volumes that they contain reflect all probabilities that emerge when particles interact. The twisting and turning of curves on the three-dimensional volume’s surface embed, in two dimensions, the mathematics required to predict outcomes.
As Dr. Spradlin explained to Quanta Magazine, “It’s a formula that you could teach to a fifth grader. You look at the collection of curves, and you count the various things that can happen to them as they go around each other.” The benefit of surfaceology is that each curve replaces many Feynman diagrams.
When the curves intersect themselves, they don’t describe particle collisions but instead the interactions of strings of energy—and therefore surfaceology is another approach to string theory. Some think it’s possible that the geometry and mathematics of the curves could eventually lead to an understanding of how the fabric of spacetime is constructed and what happens when stars run out of fuel, imploding to form black holes.
The idea that quantum memory is stored geometrically in curves emerged 40 years ago, in 1984.
Subatomic particles like neutrons, which have no electrical charge and are found in the nucleus of all atoms except hydrogen, have a quantum property called spin. Spin defines the orientation of the particle’s poles, which are influenced by magnetism in the external electromagnetic field.
For example, a particle with its north pole pointing up is said to be “spin up,” whereas the same particle with its north pole pointing down is described as “spin down.” In 1984, physicist Sir Michael Berry calculated that if the spin is slowly changed by altering the magnetic field and then returned to its original position, it causes a shift in the geometry of the wave in which the particle is located.
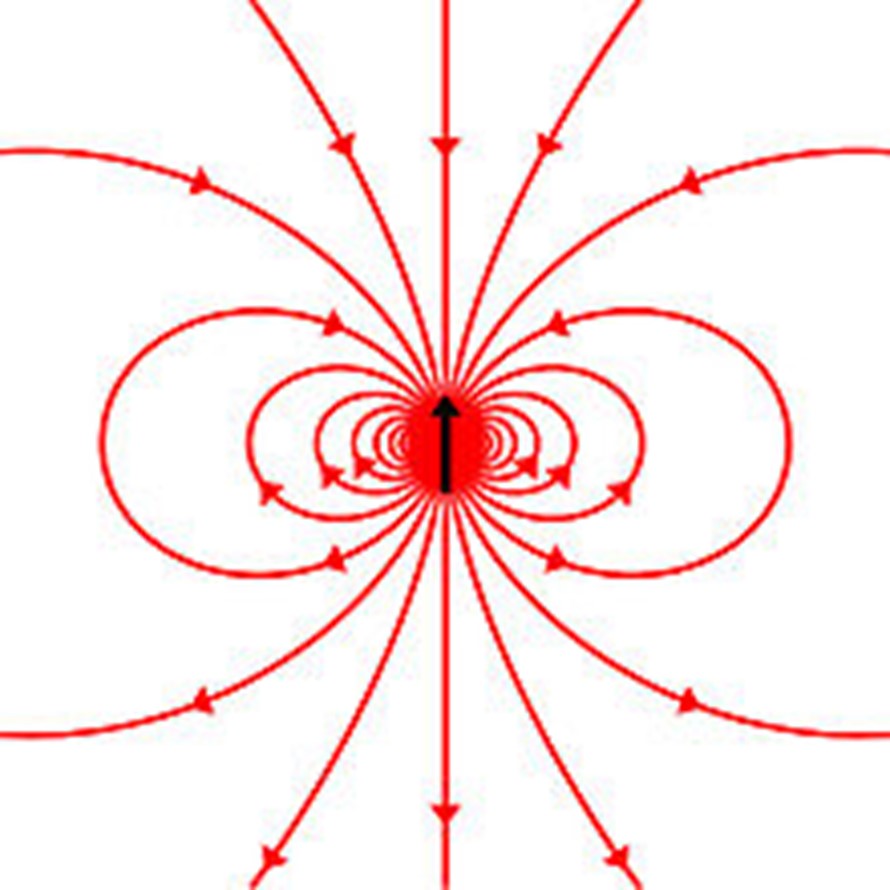
Diagram depicting the spin of a neutron, represented by the black arrow, surrounded by magnetic field lines. Image: Wikipedia .
The shift is known as a phase change, in which the angle of the particle’s wave function is altered. The phase change provides a record of the particle’s actions over time, represented in the geometry of the wave function.
Berry’s calculations were later confirmed by experiments, overturning the previously held idea that a particle’s mass, spin, energy, and momentum would be unaffected by a magnetic change that is later reversed. While quantum wave functions are not directly observable, because the act of observation changes them (see our May 2024 article The Observer Effect: Why Do Our Measurements Change Quantum Outcomes?), it is possible to compare the phases of two particles, one of which had been in a magnetic field.
The difference in the particles’ orientations is evidence of the memory of the particle that had been subjected to a phase shift in the magnetic field.
While Einstein’s theories of special relativity and general relativity, published in 1905 and 1915 respectively, made it clear that the physical universe operates in relative degrees of curvature, until Berry’s calculations it had not been thought that the large-scale phenomenon would also apply at the smallest scale of quantum particles.
As physicist Manon Bischoff wrote in How Geometry Revealed Quantum Memory (republished in Scientific American), “For me, the most impressive thing is that Berry established the new research field of geometric quantum physics by drawing on existing mathematical concepts. He didn’t have to add anything new to physics or mathematics—instead mathematics made it possible to reveal something completely unexpected in physics.”
From curves to universal memory: what next?
The discovery in 2015 that gravitational waves from the collision of massive neutron stars ripple throughout spacetime and alter the fabric of the universe (see our December 2022 article LIGO Technology May Conquer Century-long Quest to Detect Physical Memory in Spacetime) provides evidence of universal gravitational memory at the largest of scales.

Image of the supermassive black hole called Sagittarius A* at the centre of the Milky Way Galaxy taken by the Event Horizon Telescope, with lines overlaid to show the orientation of its magnetic polarization. Released in March 2024, this image represents the first time that astronomers have been able to measure polarization, a signature of magnetic fields, at a distance close to the edge of Sagittarius A* and the black hole’s event horizon, where space and time end. Image: Event Horizon Telescope Collaboration
Memory is a key function of the universe.
The famous debate over the universal law of conservation of information between physicists Leonard Susskind and Stephen Hawking, who established that black holes lose their mass in an extremely slow process of radiation, was settled by agreement that information falling into a black hole is not lost but instead imprinted as permanent memory on the black hole’s boundary, which is called the event horizon.
While gravitational waves from neutron star collisions that were discovered by LIGO are evidence of large-scale memory, in August 2023 we wrote about the discovery of a low-frequency universe-wide “hum” that is ten times weaker (see Does the Universe Have a Holographic Memory?). Physicist Dr. Jeff Hazboun told us that the hum originates from different sources than the gravitational waves discovered in 2015, possibly from the collision of black holes but also possibly from the quantum-scale interactions of particles that occurred immediately after the Big Bang.
Quantum memory, at the tiniest scale, is an emerging science.
Last month, in Major Advances in Quantum Memory Make Quantum Networks Increasingly Probable. What Comes Next?, we featured technological breakthroughs that could create and expand quantum computing memory, which will be necessary to connect large-scale networks of quantum computers. Already, scientists have devised a theoretically workable method to multiply by 1,000 times the memory capacity of today’s optical discs, using the spin states of photons of light.
The law of conservation of information states that information is neither created nor destroyed in the universe, but rather retained in universal memory. Do all of the discoveries and developments described here point to a connection between universal memory at the largest scale and at the smallest scale – and therefore possibly to the connection between general relativity and quantum mechanics?
Time, and the work of scientists like Dr. Strominger, Carolina Figueiredo, and many others, promise an intriguing answer to the question.
Your feedback helps us shape The Quantum Record just for you. Share your thoughts in our quick, 2-minute survey!
☞ Click here to complete our 2-minute survey





“Quantum Field Memory” idea?
“Every quantum field everywhere keeps faint residual echoes of every particle that ever passed through — possibly detectable, possibly exploitable — like a memory layer beneath reality.”
no formal published theory in physics frames this idea exactly this way.
Pieces exist:
• Gravitational memory effects (known),
• Vacuum fluctuations (known),
• Holographic principles (speculated),
• Quantum hysteresis in condensed matter (known),
—but they remain disconnected in theory-space.
nothing stitches this into a singular, testable principle of “universal quantum memory.”
Pass a laser through a vacuumed shielded space, then pass another laser through the same space to look for changes.
Quantum archeology:)