Accounting for each and every quantum from present to past, and future: the qubit and the order of time
What is the quantum and why does it require a different method of accounting?
Quantum accounting is not required for signals in a particular algorithm for a quantum computing application. The designers of the particular algorithm already know the order of signals in their instruction set, which is their own account. However, the algorithm designers have no way of knowing how their algorithms will interact with the rapidly increasing numbers of algorithms being designed for the quantum computer. Unlike the algorithms running in the “classical” computers in use today, which are separated from each other by wires and digital channels, quantum computing algorithms will affect each other because they all operate in the same, undifferentiable medium – which is the quantum.
Imagining the quantum
In the physics of the universe, the quantum is the smallest packet of energy that can cause change or can be changed. Since cause always precedes effect in time, and effect always contributes to subsequent causes, a minimum of two quanta are required to combine before either can have a probability to change or to be changed. The product of change, when two quanta combine, is physical matter which, in its shape (or limits), contains difference. The fact that energy and physical matter are interchangeable states of the quantum was established by Albert Einstein’s famous equation:
E=mc(1+1)
With no difference, one quantum of energy is like another and separately there is no difference in their force. The capacity of difference arises only when a quantum pair entangles, having in its geometric combinations the potential to contribute to difference. Only with a minimum of two paired quanta can energy, in varying combinations of quantum pairs, transform to physical matter that contains difference, expressed physically as resistance. Resistance requires a cause, which is the interaction that produces the difference, and an effect, which is the mass that results from the difference. In an entangled pair, one quantum is the cause and the other is the effect – but without a difference in time. Time arises in the transmission of cause and effect through three dimensions of space.
An important feature to remember is that each quantum is the same as every other quantum, and all physical matter is composed of a (usually huge) number of quanta. (Quanta is the plural of “quantum”). As a result of its universal self-similarity and its basis in all matter, in the absence of difference each quantum reacts with every other quantum in the same manner and with the same force. Therefore, when two quanta “entangle”, or join in harmonizing their causes and effects, what happens to one entangled quantum will happen to the other half of the pair.
But the story of quantum entanglement does not end with each harmonized pair – because at each of its two limits, one pair can connect with two more pairs, which can connect with four more pairs, and so on in a geometric progression of pairings.
What quantum algorithm designers cannot establish on their own is a means to prevent their signals from interacting with those of algorithms designed by others. Since there is no physical wire or digital channel to separate quanta, as algorithms begin to proliferate there will no means to ensure signal separation – other than an accurate account in which the logical sequencing of signals can be determined, free of signal interference and human judgment.
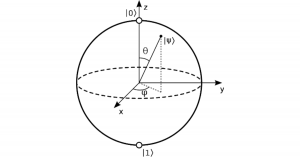
Quantum Accounting Principle I:
The present is in the middle of the qubit, and the past and future are at opposite points on the circumference
The purpose of quantum accounting is to provide an accurate record of the functional order of signals that are produced by the quantum computer and transmitted by qubits. Qubits, as discussed in Part 1 of this series, are the spherical three-dimensional quantum analogue of the binary ‘bits’ that exchange signals in our “classical” computers of today. “Functional order” means the sequence in which each instruction – or “signal” – contributes to an output, or “function”, of the computer as instructions pass from one spherical qubit to the next over time.
The quantum account of time and spherical geometry of the qubit
The inputs to the quantum account begin in a superposition, in the middle of the spherical qubit. At that point, the inputs exist in two opposite states simultaneously, each one equal to and therefore cancelling the other. The result of any combination that produces zero difference at the middle of its equal and opposite states is the part of the quantum account that we call “the present”.
The combination of opposites in the middle of the qubit is undefined, and therefore neutral to the limits of the opposed states. However, the limits of the opposites – one is the “past” and the other is the “future” in the account – contain the potential for difference in subsequent outputs as combinations of qubits accumulate over time.
Within a single qubit, the combination of opposites in superposition is always balanced in equal measure and contains a neutral middle in its output. However, the middle of one output is positioned differently in three dimensions of space relative to the middle of either or both of the previous and subsequent outputs of other qubits. It is this relative difference in the spatial position of qubits and their outputs, over time from past to future, that results in change. The limit to the rate of change of physical matter in time is the speed of light, denoted as c, which equals 299,792,458 metres per second in a vacuum.
Changes in the spatial position of outputs arise as the paired radii of one qubit in the transmission sequence orient at varying angles relative to pairs in other qubits. In their continuous rotation, differences in the angular momentum of radii pairs within and among the sequences generate change and probability in combinations of outputs.
The radius of the qubit extends to the past and future potential in time, beginning at the input of the present in the neutral middle and ending at opposite points in the qubit’s spherical circumference.
Registering difference in the diameter of the spherical qubit
The zero difference in the middle of the sphere is the singular position from which every radius that extends to one point on the circumference is equally matched by a radius that extends to the opposite point on the circumference. The two equally-matched but opposite radii combine in a straight line, which is the diameter of the sphere. The middle of the diameter is common to both radii, and therefore is not part of either radius. By excluding itself from the measurement of either limit, the zero difference in the middle of the diameter enables accurate measurement of both past and future limits. This measurement establishes signal duration and order, which is critical to record the relative positions in space and time of the middle of each qubit.
In creating a register of the order of the sequential combinations of the neutral middle in each qubit, according to the relative positions of qubits in space and time, the quantum account will contain an accurate record of the functional order of signals.
Waves and points of signals in transmission
Signalling differences and their sequences in transmission over time through the spherical geometry of the qubits produce “waves” of accumulated outputs that oscillate over time. As they pass from one qubit to the next, signalling sequences are of varying duration (“wavelength” in time) and amplitude (magnitude of the wave’s peaks and troughs), which either add to or subtract from the cumulative effect of preceding signals.
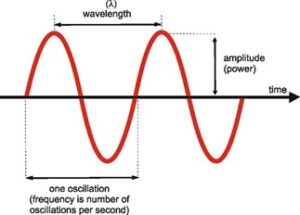
In the topology, or graph, of the analogous electromagnetic wave function (depicted here in two dimensions), the line labelled “time” is the collection of individual signals that are of zero difference where the peaks and troughs of amplitude cancel each other.
The resulting “constructive” (additive) or “destructive” (subtractive) interference in the signalling wave over time causes motion, which is a change of state, in the qubits. The physical expression of motion is measurable by differences in the angular momentum of qubit diameters, as they respond to the varying force of signal duration and amplitude passing through and among the qubits. The diameters constitute the straight line of time that divides the wavelength and frequency equally between past and future. The combinations of angular momentum establish the direction of motion in the line of time. The result is a “topology” of time by which we can plot the trajectory and force of the signalling wave through three dimensions of space.
Ratios and the circular ordering of outputs
A sphere is composed of an uncountable number of circles, all sharing a common middle and therefore a common radius. The circles, however, do not share a common diameter, since each circle forms a plane that is different from all other circular planes within the sphere. Since a circle has no defined beginning or end, determining the sequential order of outputs from one qubit to another – with each output registering at two opposite points on the circular limits of the qubit and on the diameter that connects them – is a function of ratio.
Knowledge of the ratio of circumference to diameter, where we find the two opposed radii that deliver the quantum account from the input at the middle to two circular limits of the qubit, is critical to establish the order of each signal in the sequence of signals. Signals in the quantum account are measured and recorded in the order that they occur in time. Quantum accounting records the ordinal position in time of each signal relative to every other signal – for example, the quantum account could indicate that a particular signal occurred “third”, relative to the “second” signal that preceded in its past and the “fourth” signal that follows in its future – and so on.
A ratio can also be called a “fraction”, and in the case of the circle in which the quantum signal transmits, the fraction is expressed as a mathematical constant using the Greek symbol for pi as:
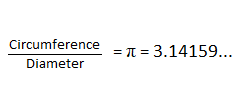
We know that π is both irrational and transcendental, with decimals that never end or establish a repeating pattern. Irrational, or what the ancients called “incommensurable”, means that the ratio forms not one fraction but instead a continued fraction without end or limit. Being transcendental, the ratio is not algebraic, meaning that it cannot be expressed in the mathematics of equivalence but instead in the relative limits of geometry.
The benefit of π as the measurement of the limit of any signal to two opposed extremes in the quantum account is that it provides no limit to the potential of signal distribution in fractions; as the decimals in π continue without end, so can the fractioning of the signals. The difficulty, however, is that we can never establish a precise fraction to define the position any one signal, and so the order of each signal must be determined relative to every other signal.
While no fractional limit can be established with certainty in the circle, using the continued fractions in the irrational ratio of π we can determine the signal ordering by understanding the geometric properties of the qubit and principles of signal transmission.
Fidelity in the quantum account in the diameter and circumference
Since all signal inputs radiate from the middle and deliver their output to the limit of the sphere, the circumference of the qubit therefore also contains the same 0 difference as the middle. The points of 0 difference – in the middle of the sphere and in its circumference – are points of balance which are essential to locate in the quantum account.
All diameters between any two opposite points of a sphere intersect at the single point in the sphere’s middle, where they form a permanent connection between the round circumference and straight diameter. All points of balance therefore reconcile to the single point of balance at the spherical middle, and since spheres are composed of circles, we can identify the point of universal reconciliation by the ratio that we know as π.
The accuracy, balance, and “fidelity” of the quantum account is complete when the sum of measured differences of all signals equals zero, in the addition and subtraction of constructive and destructive interference. The state of 0 difference – where there is no change and therefore neither addition nor subtraction – exists at all times in the geometric (or spatial) middle of the qubit and at the circumference which is the radial limit of the middle. In a state of 0 difference, the signals contain the unlimited potential of both addition and subtraction in equal and opposite measure.
Expressed in the mathematics of equals and opposites, the point of balance in the quantum account at zero is:
0 = +1/(1+1) – 1/(1+1)
and therefore the middle of the quantum account is the “arithmetic geometric mean” of the account.
Next in Introduction to the Theory of Quantum Accounting: Principle II and the triangle



