
Fractals consist of patterns that repeat at many scales of magnification. Artistic impression of a fractal structure from Pixabay.
By Mariana Meneses and James Myers
Fractals are self-similar geometric patterns that repeat at any scale of measurement.
They have long been of interest to mathematicians and physicists searching for the fundamental principles behind the differences that are everywhere in nature and numbers. Fractals are notable for their ability to be split into infinitely many parts with each resembling a reduced-size copy of the whole, and new research is revealing how fractals might actually operate in the basic structure of biology and many dynamic systems, in our brains and artificial neural networks, and in physical materials with potential application in quantum computing.
Scientists have discovered that a metabolic enzyme from the cyanobacterium Synechococcus elongatus can self-assemble into complex fractal patterns called Sierpiński triangles. This is notable because, while macroscopic fractals are common in nature, until now molecular-level fractals have only been observed in synthetic systems.

The Sierpinski triangle (on the right) is a fractal of a triangle. Image: Wikipedia
Using cryo-electron microscopy, the researchers demonstrated that the enzyme’s fractal structure is built from hexameric (six-unit) building blocks of this natural protein. They also found that various stimuli can influence the formation of these fractal complexes, which in turn can regulate the enzyme activity in a controlled lab environment. Despite this, the fractal structure might not have any functional role within the living cyanobacterium.
By reconstructing ancestral protein sequences, the researchers traced the fractal’s evolution, suggesting it evolved from non-fractal precursors likely as an accidental byproduct of evolution. This finding expands our understanding of the types of protein complexes that can exist and shows that complex, regulatable structures can evolve from simple genetic mutations.
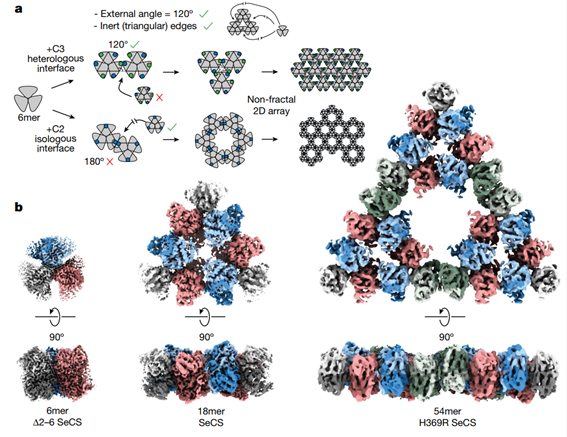
Emergence of fractal geometries in the evolution of a metabolic enzyme. Image: Franziska L. Sendker and co-authors.
In a related endeavour, researchers at MIT and four other labs have discovered an intriguing pattern in an already curious material, neodymium nickel oxide (NdNiO3).
Since NdNiO3 can act unusually as both an electrical insulator and conductor, the newly revealed pattern could lead to significant applications in artificial neurons and magnetic memory storage.
Neodymium nickel oxide is a quantum material with peculiar electronic and magnetic behaviors originating from tiny quantum effects at the atomic scale. Recent studies have unveiled surprising fractal-like arrangements within its magnetic configurations, producing geometric patterns that repeat themselves endlessly at different sizes and scales within the material’s structure.
Quantum materials show strong electronic interactions and unique orders, like superconductivity or magnetism, that can’t be explained by regular particle-based models of physics. These materials also display collective behaviors from quantum effects, like those found in ultra-cold atoms, and on a tiny scale there are complex interactions between different aspects like electric charge, spin, and the arrangement of atoms. This complexity leads to quantum entanglement and fluctuations, making quantum materials quite different from everyday materials we encounter (Wikipedia).
This unexpected discovery offers insights into the intricate nature of quantum materials, hinting at potential applications in emerging technologies like neuromorphic devices, which mimic the functionalities of biological neurons. NdNiO3’s ability to switch between electrical conduction and insulation, akin to how neurons can be active or inactive based on electrical voltage levels, holds promise for advancing quantum computing. Like the two electrical states that exist in NdNiO3, the quantum computer’s qubits — which are the fundamental units of quantum information analogous to the bits in everyday computers — can exist in two states simultaneously.
Furthermore, while the magnetic orientations in NdNiO3 distribute unequally in areas (called “domains”) throughout the material, the number of smaller domains always exceeds the number of larger domains. This repeating pattern of areas in relatively greater and lesser sizes is fractal-like, and the resulting self-similarity of the material could make it a reliable medium for storing quantum memory in magnetic orientations.
The relative sizes of magnetic domains were measured using synchrotron radiation, a technology that The Quantum Record recently reported on (see “Shedding New Light on Matter”) that holds significant promise for discovery of new properties in a variety of materials.
Although NdNiO3 isn’t directly utilized in quantum computers presently, its distinctive properties position it as a compelling subject for further exploration in advancing quantum technologies and understanding the underlying quantum phenomena within complex systems.
Fractals play a significant role in describing various natural phenomena, including snowflakes (see our article, The Mystery of Snowflakes and (Dis)Similarity in Nature), the branching patterns of trees, and the Romanesco cauliflower’s intricate structures. With diverse degrees of self-similarity, fractals illustrate the complexity and beauty of the natural world. They also offer insights into processes that unfold over time and contribute to efficient systems in nature, for example by maximizing sunlight exposure in plants and optimizing oxygenation in the human cardiovascular system.

Mandelbrot set. Image: Wolfgang Beyer
The mysteries of Mandelbrot may yield important new information on dynamic systems.
When we hear the word ‘fractal’ the first thing that often comes to mind is the Mandelbrot Set, a captivating mathematical concept born from the exploration of a simple quadratic equation. Named after mathematician Benoit Mandelbrot, who first computerized its production, the Mandelbrot set emerges through a process of iterating the quadratic function f(z) = z2 + c with various starting values. The Mandelbrot set offers a glimpse into the behavior of dynamic systems—systems that evolve and change over time—helping us to understand their complexity and operation.
Beginning in the 1970s, Benoit Mandelbrot’s pioneering work explored this set as well as other aspects of fractal geometry, and he coined the word “fractal.”As reported by Quanta Magazine, despite extensive study, fundamental questions about the Mandelbrot Set persist, particularly concerning its complex fractal boundary and the concept of local connectivity.
Functioning iteratively, the Mandelbrot set appears to have universal application, serving “as a sort of master catalog of dynamical systems — of all the different ways a point might move through space according to a simple rule.”
A significant challenge remains to prove that the Mandelbrot set is not just universally connected, but also “locally connected” which means that at any scale of magnification it looks continuously connected. This is particularly important because, like dynamic systems, not every point in the set behaves the same way: some converge to a single value, others oscillate around several values, and still other points jump between all values within defined limits.
Solving these puzzles could yield profound insights into the underlying principles of dynamic systems, enhancing our ability to predict and manipulate their behavior. This understanding is vital in numerous fields, from physics and biology to economics and engineering, where the ability to model and control dynamic systems can lead to advancements in technology, medicine, and beyond.
Math’s Famous Fractal Demystified – The Mandelbrot Set | Quanta Magazine
Fractals are in our heads.
Neuroscience research shows that the brain exhibits a fractal pattern in structure and activity, which display similar patterns when examined at a small scale (like individual neurons) or a larger scale (like brain regions).
In a 2021 study published in the journal Scientific Reports, Julian H. Smith, from the Physics Department at the University of Oregon, and colleagues highlight the intricate and fascinating ways in which neurons are structured and how their unique geometry plays a crucial role in their ability to communicate and function effectively in our brains and nervous systems.
The researchers showed that neurons, the electrically-activated cells in our brains and nervous systems, have a unique structure that resembles fractals. This fractal-like structure is seen in the branching patterns of dendrites, which are like the “arms” of the neuron that receive signals from other neurons. The study found that neurons use this fractal-like structure to optimize their connectivity with other neurons. With dendrites that branch out in a fractal pattern, neurons can efficiently connect with a large number of other neurons. This optimized connectivity is crucial for the proper functioning of our brains and nervous systems.
Understanding how neurons use fractal geometry to connect with each other can provide insights into various neurological conditions and diseases.
Changes in the fractal patterns of neurons could be linked to conditions like neurodegenerative diseases or developmental disorders. The research also suggests that knowledge of how neurons optimize their connectivity through fractal geometry can be applied to designing better medical implants that interact with neurons. By mimicking the fractal-like structure of neurons, scientists may be able to create more effective interfaces between medical devices and the nervous system.

Simulated impression of fractal patterns connecting the brain to the cosmos. Image generated using Ideogram AI.
Building on a bulk of previous research that includes the 2021 study by Smith and co-authors, a 2022 paper published in the journal Cerebral Cortex by George F Grosu, from the Department of Experimental and Theoretical Neuroscience at Transylvanian Institute of Neuroscience, Romania, and co-authors reported a potentially crucial finding about the nature and organization of the brain, and how it connects to our interactions with the world around us.
The researchers found compelling evidence that the brain’s fractal structure and scale-free dynamics play a crucial role in how we interact with our environment. They observed that the brain’s fractal organization allows for efficient processing of sensory information and adaptation to changing stimuli. For example, the brain’s ability to process dynamics at any scale enables us to respond rapidly to sensory inputs, such as detecting subtle changes in our surroundings or reacting to unexpected events.
This suggests that the brain’s fractal nature may underlie our cognitive abilities, perception, and behavior by providing a flexible and adaptive framework for processing information from the environment. In essence, the fractal brain not only reflects the complexity of our neural networks but also highlights how our brains are finely tuned to navigate and make sense of the world around us.
The researchers suggest that by understanding these fractal patterns in the brain, we can gain insights into how different parts of the brain are connected and how they work together to produce thoughts, behaviors, and perceptions. This concept of fractals helps us to see the brain as a highly interconnected and organized system, where even small details contribute to its overall functioning.
By studying these fractal patterns, scientists hope to uncover more about how the brain processes information, how it generates thoughts and behaviors, and how it adapts to different situations. This knowledge could have significant implications for understanding brain disorders, developing new treatments, and even creating advanced artificial intelligence systems inspired by the brain’s complexity.
Image generated using Ideogram AI.
An improved understanding of the brain could improve artificial neural networks.
A recently-published study by Jascha Sohl-Dickstein, from the University of California, Berkley, investigated how training neural networks is similar to creating fractals.
Imagine tweaking the settings on a fractal generator and noticing how tiny changes can completely change the pattern. Similarly, in training a neural network, adjusting even small settings can dramatically affect how well it learns. By running experiments with different setups, like using different types of data or training methods, the researchers found that the boundary between settings that make a neural network work well and those that don’t is like a fractal—it’s incredibly complex and repeats itself at different levels of detail.
They discovered this fractal pattern in various scenarios, showing that it’s a fundamental aspect of how neural networks learn. The study also explores how these fractals are different from the ones you might be familiar with, like the Mandelbrot set, because neural networks involve lots of randomness and operate in high-dimensional spaces. This research suggests that understanding these fractal-like patterns could help us improve how we train neural networks and how we use them for tasks like recognizing images or understanding language.

Fractals make us think about scale and infinity. Image generated using Ideogram AI.
Fractals are objects of many studies in mathematics.
Nash Weerasekera for Quanta Magazine dives into a math puzzle called Falconer’s conjecture, that tries to understand how points are spread out in space and the different distances between them.
Picture scattering points on a flat surface and measuring the spaces between each pair of points. Normally, you’d get various distances, but if you arrange the points in a special way, like making a grid, you’ll have fewer unique distances. The idea is to figure out the smallest number of these different distances for different arrangements of points.
This problem has fascinated mathematicians for a long time, and Falconer added to it by considering what happens when you have endless points and how their spread relates to the fractal dimension, which is a measure of how intricate a shape is. Recently, mathematicians have made strides in understanding this puzzle in higher dimensions, showing how different mathematical tools, like harmonic analysis, can help crack it. So, while Falconer’s conjecture isn’t totally solved yet, progress suggests we’re getting closer, shedding light on how fractals connect various areas of math.
Is the Cosmos a Giant Neural Network? Brain vs. Universe | How About
According to a study published in Frontiers in Physics and led by Francoise Remacle, from the Universitá di Bologna, Italy, the fascinating similarity between the cosmos and the human brain lies in their fractal structure.
Like the way the neurons in our brains form complex networks that extend from microscopic synapses to larger functional regions, the cosmic web of galaxies spans unimaginable distances, weaving together clusters, filaments, and voids on a universal scale. Despite their vast differences in size and composition, both systems exhibit self-similarity, suggesting that similar underlying principles govern their formation. This connection hints at a deeper relationship between the microcosm of neural networks and the macrocosm of cosmic structures, raising intriguing questions about the nature of complexity and organization in the universe.
The interconnectedness of fractals, spanning from quantum materials to biological structures like neurons and the complex dynamics of the human brain, reveals a fundamental pattern underlying the fabric of the universe.
From the discovery of fractal-like patterns in quantum materials such as neodymium nickel oxide to the fractal geometry of neural networks and the brain, researchers are unraveling the common thread that links disparate systems at different scales. These intricate patterns not only offer insights into the behavior of dynamic systems but also hold promise for advancing technologies like quantum computing and medical implants, while simultaneously deepening our understanding of the cosmos and the mathematical foundations that govern it.
Craving more information? Check out these recommended TQR articles:
- The Mystery of Snowflakes and (Dis)Similarity in Nature
- Quantum Ethics: There’s No Time Like the Present to Plan for the Human Future with Quantum Technology
- From Nature to Robots and Vice-Versa? Blurring the Lines Between the Real and the Virtual
- Shedding New Light on Matter: Synchrotron Radiation and Neutron Beams Probe the Tiniest Pieces of Nature
- New Insights Reveal Unexpected Patterns in Evolution of Humans and Other Species
- Getting Hold of the Atom: New Findings Illuminate What Keeps Matter, and Us, Together
- The Observer Effect: Why Do Our Measurements Change Quantum Outcomes?
- Science Probes the Frontiers of Quantum and Mathematical Consciousness



